Câu 1.Tìm điều kiện của x để \(\sqrt{\dfrac{-1}{1-x}}\) có nghĩa?
A. x < 1 B. x > 1 C. x ≥ 0 D. x ≤ 1
Câu 2. Hàm số \(y=\sqrt{2015-m}.x+5\) là hàm số bậc nhất khi:
A. m ≤ 2015 B. m < 2015 C. m > 2015 D. m ≥ 2015
Câu 3. Tìm k để đường thẳng \(y=\left(2k+1\right)x+3\) nghịch biến trên R.
A. k ≤ \(\dfrac{-1}{2}\) B. k < \(\dfrac{-1}{2}\) C. k < -1 D. k ≤ -1
Câu 4. Cho hàm số: \(y=f\left(x\right)=\dfrac{2}{x+1}\) .Biến số x có thể có giá trị nào sau đây:
A. x ≤ -1 B. x ≥ -1 C. x ≠ 0 D. x ≠ -1

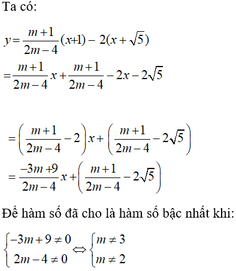
C1:
\(1-x>0\Leftrightarrow x< 1\)
C2:
\(2k+1< 0\)
\(\Leftrightarrow k< \dfrac{-1}{2}\)
C3:
\(x+1\ne0\Leftrightarrow x\ne1\)
1B
2B
3B
4D