Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Mặt cầu (S) có tâm I (1;0;-2) và bán kính R=2.
Đường thẳng d đi qua điểm N (2; 0; m-1) và có véc tơ chỉ phương 
Điều kiện để d cắt (S) tại hai điểm phân biệt là d (I; (d))<R
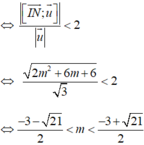
Khi đó, tiếp diện của (S) tại A và B vuông góc với IA và IB nên góc giữa chúng là góc (IA;IB).
Vậy T= {-3;0}. Tổng các phần tử của tập hợp T bằng -3.
Chọn đáp án C
STUDY TIP |
Ta lập phương trình đường thẳng đi qua hai tiếp điểm của hai tiếp tuyến với (C) bằng phương pháp gián tiếp |
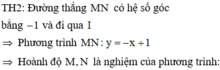
- Xét phương trình hoành độ giao điểm : \(mx-4=-mx-4\)
\(\Leftrightarrow2mx=0\)
\(\Leftrightarrow x=0\)
\(\Rightarrow y=-4\)
=> Tọa độ điểm ( 0; - 4 )
- d1 cắt trục hoành tại điểm : \(\left(\dfrac{4}{m};0\right)\)
- d2 cắt trục hoành tại điểm : \(\left(-\dfrac{4}{m};0\right)\)
=> Tam giác đó là tam giác cân .
\(\Rightarrow S=\dfrac{1}{2}.\left|-4\right|.\left|\dfrac{8}{m}\right|=\left|\dfrac{16}{m}\right|>8\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{16}{m}< -8\\\dfrac{16}{m}>8\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m\in\left(-2;0\right)\\m\in\left(0;2\right)\end{matrix}\right.\)
Vậy \(S=\left\{1\right\}\)
Gọi S là tập hợp các giá trị của m để đường thẳng y= (m-2) +3 cắt hai trục tọa độ tạo thành 1 tam giác AOB vuông cân. Tính tổng các phần tử của S:
A. 1 B.2 C.3 D.4
C