Chứng minh rằng : \(\left(2005+2005^2+2005^3+...+2005^{10}\right)\) chia hết cho 2006
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CP
1
BD
12 tháng 11 2017
a)M=2005+20052 +.....+200510
=>M=(2005+20052 )+.....+(20059 +200510 )
=>M=2005(1+2005)+.....+20059 (1+2005)
=>M=2005*2006+.....+20059 *2006
=>M=2006(2005+...+20059 ) chia hết cho 2006(đpcm)
b)A=3+32 +....+3100
=>A=(3+32 +33 +34)+....+(397 +398 +399 +3100 )
=>A=3(1+3+32 +33 )+....+397 (1+3+32 +33 )
=>A=3*40+...+397 *40
=>A=40(3+...+397 ) chia hết cho 40(đpcm)
NB
0
5 tháng 9 2021
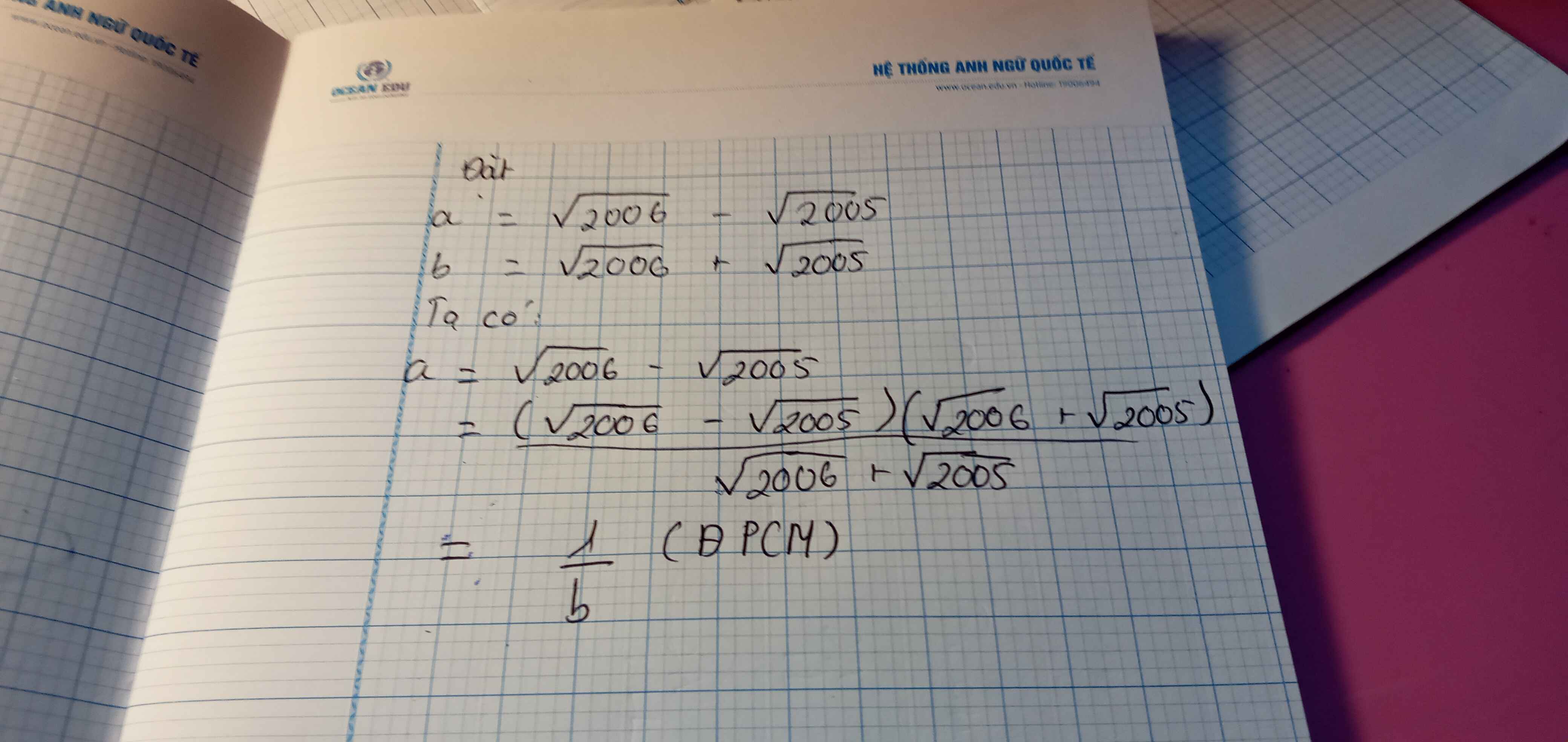
Đặt \(a=\sqrt{2006}-\sqrt{2005};b=\sqrt{2006}+\sqrt{2005}\)
Ta có
\(a=\sqrt{2006}-\sqrt{2005}=\dfrac{\left(\sqrt{2006}-\sqrt{2005}\right)\left(\sqrt{2006}+\sqrt{2005}\right)}{\sqrt{2006}+\sqrt{2005}}=\dfrac{1}{b}\)
\(\RightarrowĐfcm\)
2005+20052+20053+...+200510
=2005.(1+2005)+20053.(1+2005)+...+20059.(1+2005)
=2005.2006+20053.2006+...+20059.2006
=2006.(2005+20053+...+20059)
=>2005+20052+20053+...+200510 chia hết cho 2006
= 2005.(1+2005)+20052.(1+2005)+...+20059.(1+2005)
= 2006.(2005+20052+...+20059)
=> tổng trên chia hết cho 2006
nhầm chút