Cho tam giác ABC vuông ở A có góc B bằng 60 độ.Tia phân giác của góc ABC cắt AC ở E.Kẻ AH vuông góc với BC (H thuộc BC).
a) Chứng minh:tam giác ABE=tam giác HBE
b) Chứng minh HB=HC
c) từ H kẻ đường thẳng song song với BE cắt AC ở K.Chứng minh tam giác EHK là tam giác đều.
d) Gọi I là giao điểm của BA và HE.Chứng minh IE>EH
HELP ME MAI ĐI THI RÙIIIIIII !!!

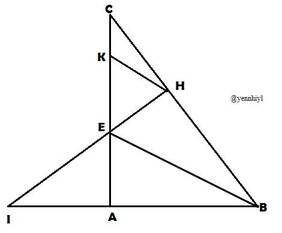
Bạn tự vẽ hình nhé. Tại mình thấy đề AH vuông góc BC hơi sai nên sẽ sửa là EH nha.
Giải
a, Vì EH \(\perp BC\)( gt ) \(\Rightarrow\)\(\Delta HBE\)vuông tại H.
Xét \(\Delta\)vuông ABE và \(\Delta\) vuông HBE, có :
BE : cạnh chung
góc ABE = góc HBE ( BE là tpg góc ABC )
\(\Rightarrow\)\(\Delta\)vuông ABE = \(\Delta\) vuông HBE ( cạnh huyền góc nhọn )
b, Ta có : BA=BH ( \(\Delta\) vuông ABE = \(\Delta\) vuông HBE ) \(\Rightarrow\) \(\Delta BAH\) cân tại B ( đ/n )
Mà góc ABC = 60o ( gt ) \(\Rightarrow\) \(\Delta BAH\) đều.
\(\Rightarrow\)AB=AH=BH ( đ/n )
Xét \(\Delta\) vuông ABC, có :
góc ABC + góc BCA = 90o ( 2 góc phụ nhau )
\(\Rightarrow\)60o + góc BCA = 90o \(\Rightarrow\)góc BCA = 30o
Mà góc EBH = 30o ( vì BE là tpg góc ABC , góc ABC = 60o )
\(\Rightarrow\)góc EBC = góc BCA ( =30o )
\(\Rightarrow\)\(\Delta\)BEC cân tại E ( t/c ) \(\Rightarrow\)BE = EC ( đ/n )
Xét \(\Delta\) vuông HEB và \(\Delta\) vuông HEC , có :
BE=EC ( cmt )
góc EBH = góc ECH ( cmt )
\(\Rightarrow\)\(\Delta\)vuông HEB = \(\Delta\) vuông HEC ( cạnh huyền góc nhọn )
\(\Rightarrow\)BH = CH ( 2 cạnh tương ứng )
c, Xét \(\Delta\) vuông ABE , có :
góc ABE + góc AEB = 90o ( 2 góc phụ nhau ), mà góc ABE = 30o ( BE là tpg góc ABC )
\(\Rightarrow\)góc AEB = 60o
Ta có : góc AEB = góc HEB = 60O( \(\Delta\) vuông ABE = \(\Delta\) vuông HBE )
Mà BE // HK ( gt ) \(\Rightarrow\) góc HEB = góc EHK = 60o( 2 góc so le trong )
Vì BE // HK ( gt ) \(\Rightarrow\) góc AEB = góc EKH = 60o ( 2 góc đồng vị )
Xét \(\Delta EHK\) , có :
góc EHK + góc EKH + góc KEH = 180o ( tổng 3 góc trong tam giác )
\(\Rightarrow\)60o + 60o + góc KEH = 180o
\(\Rightarrow\)góc KEH = 60o
Ta nhận thấy trong tam giác EKH cả 3 góc đều bằng 60o ( cmt )
\(\Rightarrow\)\(\Delta EKH\)là tam giác đều ( t/c)
d, Xét \(\Delta\) AEI và \(\Delta HEC\) , có :
góc EAI = góc EHC ( = 900 )
AE=EH ( \(\Delta\) vuông ABE = \(\Delta\) vuông HBE )
góc AEI = góc HEC ( 2 góc đối đỉnh )
\(\Rightarrow\Delta AEI=\Delta HEC\)( g-c-g )
\(\Rightarrow\)EI = EC ( 2 cạnh tương ứng )
Xét \(\Delta\) vuông HEC, có :
EC > EH ( cạnh huyền > cạnh góc vuông ) , mà EC = EI ( cmt )
\(\Rightarrow\)EI hay IE > EH ( đpcm )