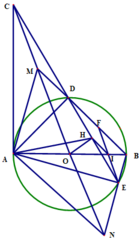
cho (O) đường kính AB và \(C\in\left(O\right)\)sao cho AC > BC. Từ O vẽ đường thẳng vuông góc với AC tại H. Qua A vẽ tiếp tuyến Ax của (O) cắt tia OH tại D. Cạnh BD cắt (O) tại E
1) cm tam giác ABC vuông, HA = CH
2) cm DC là tiếp tuyến của (O)
3) cm HD.DO = DE.DB và \(\widehat{DHE}=\widehat{DBA}\)
4) trên tia đối của tia EA lấy F sao cho E là trung điểm của AF.Từ F vẽ đường thẳng vuông góc với AD tại K.FK cắt BC tại M.cm MH = MK