Cho tam giác ABC vuông tại A . Góc C = 40 độ . Vẽ tia phân giác AD và AH vuông góc với BC (D,H thuộc BC ). Tính góc HAD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1 tháng 11 2017
Vì góc A = 90o , AD là tia phân giác góc A nên góc BAD = góc DAC = 90/2 = 45o.
Vì AH vuông góc với BC nên góc AHC=900
Trong tam giác HAC có : (góc) HAC + HCA + AHC = 180o
===> góc HAC + 400+900 = 1800
===> góc HAC = 500
Vì góc HAC > góc DAC (900>450) nên tia AD nằm giữa hai tia AC và AH
===> góc HAD + góc DAC = góc HAC
====> góc HAD + 450=500
===> góc HAD = 50
16 tháng 9 2016
Ta có hình vẽ:
Kẻ đường thẳng aa' đi qua điểm A sao cho aa' // BC
Vì AD là tia phân giác của CAB
=> \(CAD=DAB=\frac{CAB}{2}=\frac{90^o}{2}=45^o\)
Ta có: ACB = CAa' = 40o (so le trong)
Mà CAa' + CAD = DAa'
=> 40o + 45o = DAa'
=> DAa' = 85o
Do AH vuông góc với BC; aa' // BC => AH vuông góc với aa'
=> HAa' = 90o
Lại có: DAa' + HAD = HAa'
=> 85o + HAD = 90o
=> HAD = 90o - 85o
=> HAD = 5o
TT
1 tháng 11 2017
Vì góc A = 90o , AD là tia phân giác góc A nên góc BAD = góc DAC = 90/2 = 45o.
Vì AH vuông góc với BC nên góc AHC=900
Trong tam giác HAC có : (góc) HAC + HCA + AHC = 180o
===> góc HAC + 400+900 = 1800
===> góc HAC = 500
Vì góc HAC > góc DAC (900>450) nên tia AD nằm giữa hai tia AC và AH
===> góc HAD + góc DAC = góc HAC
====> góc HAD + 450=500
===> góc HAD = 50
13 tháng 8 2021
a: Xét ΔADC có
\(\widehat{ADC}+\widehat{DAC}+\widehat{C}=180^0\)
\(\Leftrightarrow\widehat{ADH}=180^0-30^0-45^0\)
hay \(\widehat{ADH}=105^0\)
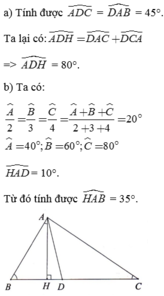
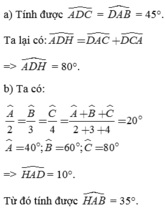
Tam giác ABC vuông tại A
=>góc BAC=90°
AD là tia phân giác của tam giác ABC
=>góc BAD=góc CAD=góc BAC/2=45°
Ta lại có,tam giác CAH vuông tại H( vì AH_|_BC theo gt)
=> góc AHC=90°
Xét tam giác vuông ACH,có:
góc HAC =180°-(góc AHC+góc ACH)
=180°-(90°+40°)=50°
=>góc HAD=góc HAC-góc DAC
=50°-45°
=5°
Ta có
tam giác AHC có
HAC+ AHC+HCA=180 nên HAC=180-AHC-HCA=180-90-40=50
Tam giác DAC có BAD=DAC=45( AD là tia phân giác)
Mà HAD+DAC=HAC nên HAD=5