cho tam giác DEF vuông tại D. Điểm H là trung điểm của EF. Trên tia đối của HD lấy I sao cho HD=HI. CMR DH =1/2. EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NH
15 tháng 11 2019
Vì M là trung điểm của EF => ME = MF
Xét △MDE và △MIF
Có : ME = MF (gt)
DME = FMI (2 góc đối đỉnh)
MD = MI (gt)
=> △MDE = △MIF (c.g.c)
=> DE = IF (2 cạnh tương ứng)
Và DEM = MFI (2 góc tương ứng)
Mà 2 góc này nằm ở vị trí so le trong
=> DE // IF (dhnb)
b, Vì △MDE = △MIF (cmt)
=> DE = IF (2 cạnh tương ứng)
Xét △HDE vuông tại H và △HGE vuông tại H
Có: HD = HG (gt)
HE : cạnh chung
=> △HDE = △HGE (cgv)
=> DE = GE (2 cạnh tương ứng)
Mà DE = IF (cmt)
=> EG = IF (đpcm)
24 tháng 12 2020
a) Xét △DEM và △KFM có
DM=KM(giả thiết)
góc DME=góc KMF(2 góc đối đỉnh)
EM=MF(Vì M là trung điểm của EF)
=>△DEM =△KFM(c-g-c)
=> góc MDE=góc MKF (2 góc tương ứng)
hay góc EDK= góc EKD mà 2 góc này là 2 góc so le trong bằng nhau của đường thẳng DK cắt 2 đường thẳng DE và KF
=>DE//KF
b) ta có DH⊥EF hay DP⊥EF => góc DHE =góc PHE =90 độ
Xét △DHE (góc DHE=90 độ)△PHE(góc PHE=90 độ) có
HD=HP
HE là cạnh chung
=> △DHE= △PHE(2 cạnh góc vuông)
=> góc DEM=góc PEM
=> EH là tia phân giác của góc DEP
hay EF là tia phân giác của góc DEP
vậy EF là tia phân giác của góc DEP
30 tháng 3 2021
a) Áp dụng định lí Pytago vào ΔDEF vuông tại D, ta được:
\(EF^2=DE^2+DF^2\)
\(\Leftrightarrow EF^2=9^2+12^2=225\)
hay EF=15(cm)
Vậy: EF=15cm
18 tháng 3 2023
`a,` Xét Tam giác `DEH` và Tam giác `DFH` có:
`DE=DF (\text {Tam giác ABC cân tại A})`
`\widehat{DEF}=\wide{DFE} (\text {Tam giác ABC cân tại A})`
`HE=HF (g``t)`
`=> \text {Tam giác DEH = Tam giác DFH (c-g-c)}`
`b, \text {Vì Tam giác DEH = Tam giác DFH (a)}`
`-> \widehat{DHE}= \widehat{DHF} (\text {2 góc tương ứng})`
`\text {Mà 2 góc này nằm ở vị trí đồng vị}`
`->\widehat{DHE}+ \widehat{DHF}=180^0`
`-> \widehat {DHE}= \wideha{DHF}=180/2=90^0`
`-> DH \bot EF`
`c,` Mình xp sửa đề là: \(\text{"Trên tia ĐỐI của DH lấy điểm K sao cho HD=HK"}\)
Xét Tam giác `DHE` và Tam giác `FHK` có:
`DH=HK (g``t)`
`\widehat{DHE}=\widehat{FHK} (\text {2 góc đối đỉnh})`
`HE=HF (g``t)`
`=> \text {Tam giác DHE = Tam giác FHK (c-g-c)}`
`-> \widehat{DEF}=\widehat{EFK} (\text {2 góc tương ứng})`
`\text {Mà 2 góc này nằm ở vị trí sole trong}`
`-> DE`//`FK (\text {tính chất đt' song song})`
18 tháng 3 2023
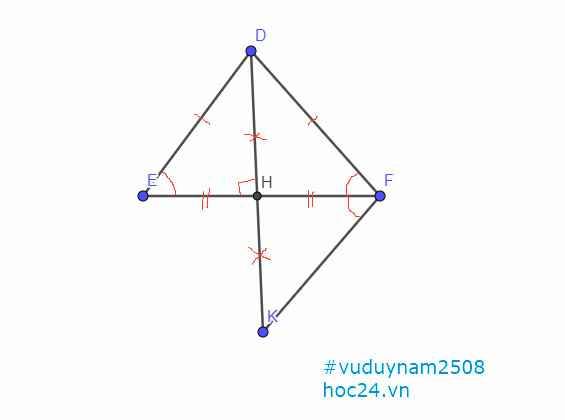
Cho tam giác DEF cân tại D,H là trung điểm EF
a)Chứng minh tam giác DEH = tam giác DFH
b)Chứng minh DH vuông góc với EF
c)Trên tia DH lấy điểm K sao cho HD = HK.Chứng minh DE // với FK
help me mình cần rất gấp.