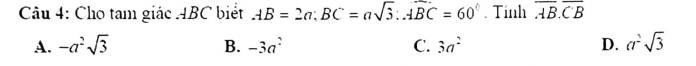Mình xin cách giải câu này với ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
5 tháng 4 2021
Để làm dạng này , bạn làm như sau :
Vì bạn biết 1 giờ = 60 phút; 1 phút =60 giây nên là
Trước hết bạn lấy số 0,8325 (số chỉ giờ) nhân 60 nhé = 49,95
Bạn lấy phần nguyên của nó trước dấu phẩy là 49 , điền vảo chỗ chấm trước phút.
Cái phần thập phân sau dấu phẩy là 0,95 bạn tiếp tục nhân 60 = 57.
Bạn điền 57 vào phần chỗ chấm trước giây.
Vậy 0,8325 giờ=49 phút 57 giây
1 tháng 3 2022
a: 4/25=16/100
-7/4=-175/100
9/50=18/100
b: -7/10=-28/40
11/20=22/40
-10/40=-10/40
c: 5/18=10/36
7/12=21/36
11/6=66/36
NT
1
30 tháng 12 2021
a: \(=\dfrac{x+2}{x+2}=1\)
b: \(=\dfrac{2x+6}{x+3}=2\)
NL
3
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
15.
\(\Delta'=m^2+m-2>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -2\end{matrix}\right.\)
Đáp án B
16.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow\dfrac{\pi}{4}< \dfrac{a}{2}< \dfrac{\pi}{2}\Rightarrow\dfrac{\sqrt{2}}{2}< sin\dfrac{a}{2}< 1\Rightarrow\dfrac{1}{2}< sin^2\dfrac{a}{2}< 1\)
\(sina=\dfrac{3}{5}\Leftrightarrow sin^2a=\dfrac{9}{25}\Leftrightarrow4sin^2\dfrac{a}{2}.cos^2\dfrac{a}{2}=\dfrac{9}{25}\)
\(\Leftrightarrow sin^2\dfrac{a}{2}\left(1-sin^2\dfrac{a}{2}\right)=\dfrac{9}{100}\Leftrightarrow sin^4\dfrac{a}{2}-sin^2\dfrac{a}{2}+\dfrac{9}{100}=0\)
\(\Rightarrow\left[{}\begin{matrix}sin^2\dfrac{a}{2}=\dfrac{1}{10}< \dfrac{1}{2}\left(loại\right)\\sin^2\dfrac{a}{2}=\dfrac{9}{10}\end{matrix}\right.\)
\(\Rightarrow sin\dfrac{a}{2}=\dfrac{3\sqrt{10}}{10}\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2021
17.
Áp dụng công thức trung tuyến:
\(AM=\dfrac{\sqrt{2\left(AB^2+AC^2\right)-BC^2}}{2}=\dfrac{\sqrt{201}}{2}\)
18.
\(\Leftrightarrow x^2+2x+4>m^2+2m\) ; \(\forall x\in\left[-2;1\right]\)
\(\Leftrightarrow m^2+2m< \min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)\)
Xét \(f\left(x\right)=x^2+2x+4\) trên \(\left[-2;1\right]\)
\(-\dfrac{b}{2a}=-1\in\left[-2;1\right]\) ; \(f\left(-2\right)=4\) ; \(f\left(-1\right)=3\) ; \(f\left(1\right)=7\)
\(\Rightarrow\min\limits_{\left[-2;1\right]}\left(x^2+2x+4\right)=f\left(1\right)=3\)
\(\Rightarrow m^2+2m< 3\Leftrightarrow m^2+2m-3< 0\)
\(\Rightarrow-3< m< 1\Rightarrow m=\left\{-2;-1;0\right\}\)
Đáp án C
