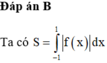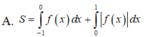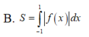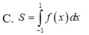cho x > 0, y >0 và x+y <=4:3 . tìm gtnn của biểu thức : S = x+y +3:4x+3:4y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
1
5 tháng 8 2016
1/x+1/y-1/z=(yz+xz-xy)/(xyz)=0 vì x,y,z#0 =>yz+xz-xy=0
x^2 + y^2 +z^2=(x+y-z)^2 +2(xz+yz-xy)=4
DT
1
28 tháng 8 2019
Ta có:\(x^2+4y+4=0;y^2+4z+4=0;z^2+4x+4=0\)
\(\Leftrightarrow\left(x^2+4y+4\right)+\left(y^2+4z+4\right)+\left(z^2+4x+4\right)=0\)
\(\Leftrightarrow x^2+4x+4+y^2+4y+4+z^2+4z+4=0\)
\(\Leftrightarrow\left(x+2\right)^2+\left(y+2\right)^2+\left(z+2\right)^2=0\)
Mà\(\left(x+2\right)^2\ge0;\left(y+2\right)^2\ge0;\left(z+2\right)^2\ge0\)
\(\Leftrightarrow\left(x+2\right)^2+\left(y+2\right)^2+\left(z+2\right)^2\ge0\)
Dấu "=" xảy ra\(\Leftrightarrow\hept{\begin{cases}x+2=0\\y+2=0\\z+2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=-2\\y=-2\\z=-2\end{cases}\Leftrightarrow}x=y=z=-2}\)
Vậy\(x^{10}+y^{10}+z^{10}=x^{10}+x^{10}+x^{10}\)
\(=3\cdot x^{10}=3\cdot\left(-2\right)^{10}=3\cdot1024=3072\)
TP
1
19 tháng 4 2016
x-y-z=0
=> x=y+z
y=x-z
-z=y-x
B=(1-z/x)(1-x/y)(1+y/z)
B=((x-z)/x)((y-x)/y)((z+y)/z)
B=(y/x)(-z/y)(x/z)
B=(-zyx)/(xyz)
B=-1
24 tháng 7 2016
Áp dụng bất đẳng thức \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\)ta có \(A=\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}=\frac{4}{2a}=\frac{2}{a}\)
Min A = 2/a tại x = y = a
MN
0
PT
1
CM
25 tháng 8 2019
Ta có: x – y = x.y ⇒ x = x.y + y = y.(x + 1) (1)
Suy ra: x : y = y.(x + 1) : y = x + 1 (2)
Theo giả thiết, x : y = x – y nên từ (2) suy ra:
⇒ x – y = x + 1 ⇒ y = −1
Thay y = - 1 vào (1) ta được:
x = (-1)(x + 1) ⇒ x = − x – 1 ⇒ 2x = −1 ⇒ x = (-1)/2
Vậy x = −1/2; y = −1.
