Cho S=2+4+6+...+100. Tính tổng S.Từ đó tính tổng các chữ số của S.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(S=1+3^1+3^2+3^3+...+3^{30}\)
\(3S=3+3^2+3^3+...+3^{31}\)
\(3S-S=3^{31}-1\)
\(2S=3^{4.7+3}-1\)
\(2S=81^7.27-1\)
\(2S=\overline{......1}.27-1\)
\(2S=\overline{......7}-1=\overline{......6}\)
\(S=\overline{........3}\)
Vậy chữ số tận cùng của S là 3=> S không phải là số chính phương
cho tổng S=1+3+32+33+...+330
tìm chữ số tận cùng của S.Từ đó ta suy ra Skhong phải là số chính phương

S=1+3+32+...+330
3S= 3+32+33+...+331
2S=331-1
331=34kx33=...1x...7=....7
=> chữ số tận cùng của 2S =...7-1=...6
=> chữ số tận cùng của S là ...8 hoặc...3 (ko là SCP)
Ta có S = 1 + 3 + 32 + 33 + .... + 330
3S = 3 + 32 + 33 + 34 + .... + 331
3S - S = (3 + 32 + 33 + 34 + ..... + 331) - (1 + 3 + 32 + 33 + ..... + 330)
2S = 331 - 1
Lại có 3311 = (34)7 x 33 = (........1)7 x 27 = (.......1) x 27 = (....7) => 2S có c/s tận cùng là 7 - 1 = 6
=> S có c/s tận cùng là 3 hoặc 8 mà số chính phương ko có tận cùng là 3 hoặc 8 => S ko phải số chính phương
ấn đúng cho mk nha các bạn!!!

1 số các số hạng là:(100-2):2+1=50 Tổng các số đó là:(100+2).50:2=2550 2 các số có 3 c/s là:100,101,102,..........,999 số phần tử là:(999-100):1+1=900 tổng là:(999+100).900:2=494550 3 là mk đag bận nên k thể trloi bn mog bn thông cảm khi nào rảnh thì mk sẽ giải hộ bn nha mk mog là bn lm đúng hết bài

Gọi số đó là \(\overline{abcdef}\Rightarrow a+b+c+d+e+f=1+2+3+4+5+6=21\)
Mặt khác \(a+b+c=d+e+f-1\)
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=10\\d+e+f=11\end{matrix}\right.\)
\(\Rightarrow\left(a;b;c\right)=\left(1;3;6\right);\left(1;4;5\right);\left(2;3;5\right)\)
Số số thỏa mãn: \(3.\left(3!.3!\right)=108\)
Xác suất: \(P=\dfrac{108}{6!}=\dfrac{3}{20}\)

Ta có tính chất: Hiệu của một số với tổng các chữ số của nó chia hết cho 9
( xem cách chứng minh tại link Câu hỏi của Nguyễn Phương Chi - Toán lớp 6 - Học toán với OnlineMath )
Do đó ta có:
\(A-S\left(A\right)⋮9\)
\(S\left(A\right)-S\left(S\left(A\right)\right)⋮9\)
\(S\left(S\left(A\right)\right)-S\left(S\left(S\left(A\right)\right)\right)⋮9\)
=> Cộng lại và triệt tiêu ta có: \(A-S\left(S\left(S\left(A\right)\right)\right)⋮9\)(1)
Ta có: \(A=2^{100}=2.2^{99}=2.8^{33}\)=> Số chữ số của A < 34
=> \(S\left(A\right)< 34.9=306\)
=> \(S\left(S\left(A\right)\right)< 3.9=27\)
=> \(S\left(S\left(S\left(A\right)\right)\right)< 2.9=18\) (2)
Mặt khác \(A=2^{100}=2.2^{99}=2.8^{33}\equiv2\left(-1\right)^{33}\equiv-2\equiv7\left(mod9\right)\)
=> \(A-7⋮9\)(3)
Từ (1); (2); (3) => S(S(S(A))) có thể bằng 7 hoặc 16
=> S(S(S(S(A)))) = 7
:)))) . Bài này thú vị quá! <3

n(S)=6!
Để thỏa mãn yêu cầu đề bài thì cần chọn ra 3 số có tổng là 12
=>Số trường hợp thỏa mãn là (1;5;6); (2;4;6); (3;4;5)
=>Có 3*3!*3!
=>P=3/20

Chọn B
Gọi số cần tìm thỏa mãn điều kiện bài toán là a b c d e f ¯ trong đó a,b,c,d,e,f ∈ S và đôi một khác nhau. Theo bài ra ta có
![]()
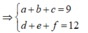
Có ![]()
![]() .
.
Ta có các cặp 3 số khác nhau từ S có tổng bằng 9 là ![]() .
.
![]()
![]()
![]()