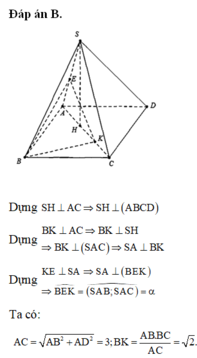
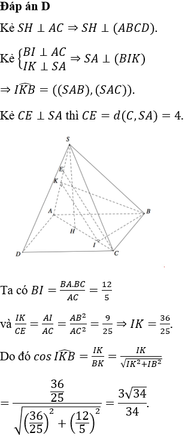
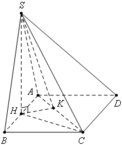
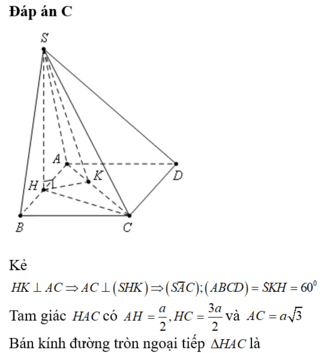
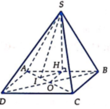
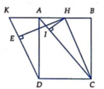
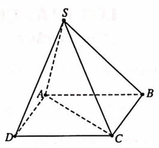
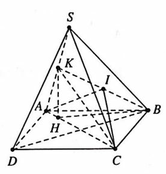
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB \(=\sqrt{6},AD=\sqrt{3}\), tam giác SAC nhọn và nằm trong mặt phẳng vuông góc với đáy. Biết hai mặt phẳng (SAB), (SAC) tạo
với nhau góc \(\alpha\) thỏa mãn \(tan\alpha=\dfrac{3}{4}\) và cạnh SC = 3. Thể tích khối S.ABCD bằng:
A.\(\dfrac{4}{3}\) B.\(\dfrac{8}{3}\) C.\(3\sqrt{3}\) D.\(\dfrac{5\sqrt{3}}{3}\)



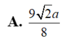
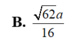
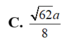
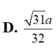

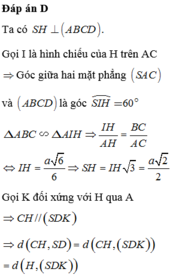



\(A.\dfrac{4}{3}\)
Tham khảo cách làm tương tự: https://moon.vn/hoi-dap/cho-hinh-chop-sabcd-co-day-abcd-la-hinh-chu-nhat-voi-ab-sqrt-6-ad-sqrt-3-tam-giac-sa-664143