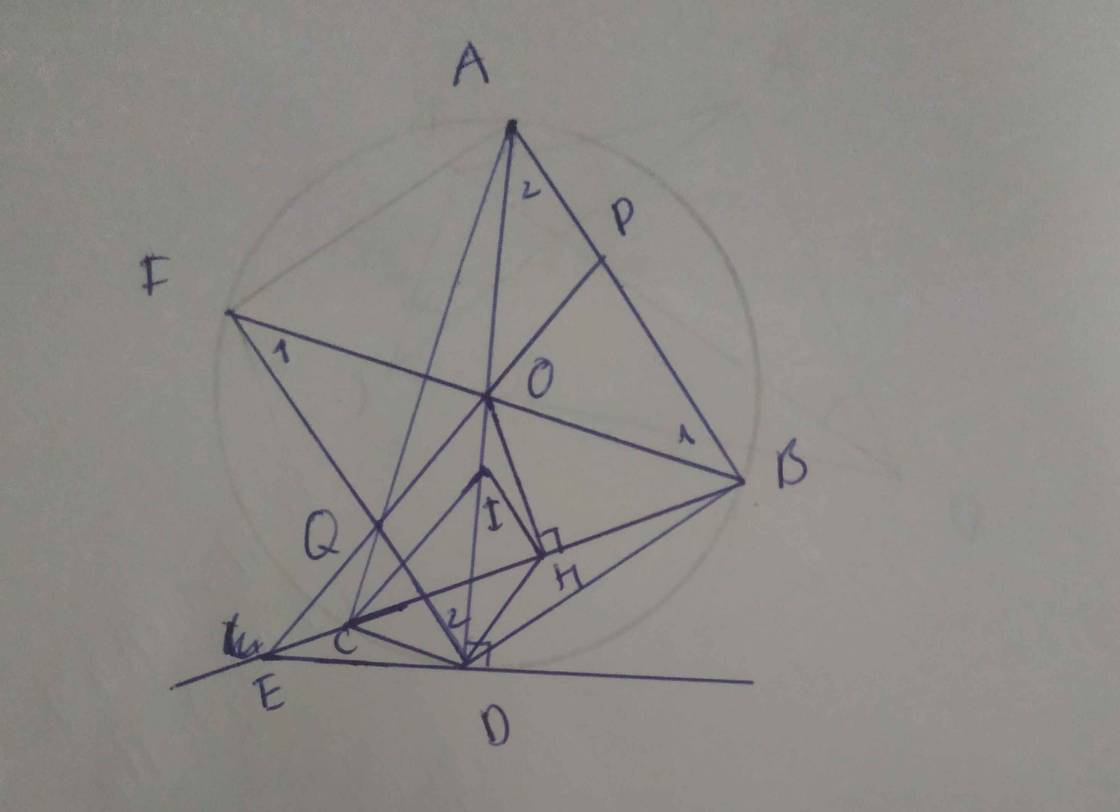
Cho đường tròn (O) á kinks R ngoại tiếp tam giác ABC có 3 góc nhọn. Ccá tiếp tuyến của (O) tại B,C cắt nau tại P.Gọi D,E tương ứng là chân cá đường cuông góc hạ từ P xuống AB,AC và M là trung điểm BC.
a) Chứng minh rằng \(\widehat{MEP}=\widehat{MDP}\)
b) Gỉa sử B,C cố định và A chạy trên ddwonwgf tròn (O) sao cho tam giác ABC luôn là tam giác có ba góc nhọn. Chứng minh rằng DE luôn đi qua 1 diểm cố định