Câu 4: Cho tam giác ABC vuông tại A có AB= 6 cm, BC = 10 cm. Trên tia đối của tia AB lấy điểm D sao cho A là trung điểm của đoạn thẳng BD. Gọi K là trung điểm của cạnh BC, đường thẳng DK cắt cạnh AC tại M. Đường trung trực d của đoạn thẳng AC cắt đường thẳng DC tại Q.
a,Tính AC, MC.
b, So sánh các góc của tam giác ABC.
c, Chứng minh tam giác BCD cân.
d, Chứng minh ba điểm B, M, Q thẳng hàng
Câu 5: Chứng minh đa thức x^2+x+1 ko có nghiệm.
GIÚP MÌNH VỚI MÌNH ĐANG CẦN GẤP!
CẢM ƠN TRƯỚC NHÉ!

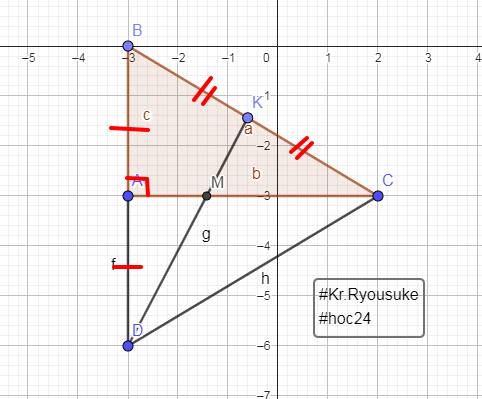





a,AD ĐL pytago vào \(\Delta ABC\)vuông tại A có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC^2=BC^2-AB^2\)
\(\Rightarrow AC^2=10^2-6^2\)
\(\Rightarrow AC^2=64\)
\(\Rightarrow AC=\sqrt{64}=8\left(cm\right)\)
Xét \(\Delta BCD\)có: A là trung điểm của BD
K là trung điểm của BC
AC giao DK tại M
=>M là trọng tâm của \(\Delta BCD\)
\(\Rightarrow MC=\frac{2}{3}AC=\frac{2}{3}.8=5,3\left(cm\right)\)
b.Ta có:\(AB< AC< BC\)
\(\Rightarrow\widehat{BAC}>\widehat{ABC}>\widehat{ACB}\)
c.Ta có:\(\widehat{A}=90^o\)và A là trung điểm của BD
=>AC là đường trung trưc của BD
=>CB=CD
=>\(\Delta BCD\)cân tại C
d. bạn tự cm \(\Delta ABC=\Delta ADC\left(c.g.c\right)\)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}\)(2 g.t.ư) (1)
Q là ttruc của AC=>QA=QC
=> tg AQC cân tại Q
=>\(\widehat{A_1}=\widehat{C_1}\)(2)
Từ (1) và (2)=>\(\widehat{C_1}=\widehat{A_1}\)
Mà 2 góc này ở VT SLT=>AQ//BC(3)
Lại có:A là trung điểm của BD(4)
Từ (3) và (4) => AQ là đường trb của tg BCD
=>Q là tđ củaDC
=>BQ là đường ttuyen của tgBCD
Mà M là trọng tâm của tg BCD
=> thẳng hàng