Ai giải giúp mik bài hình đc ko mik đang rất gấp ạ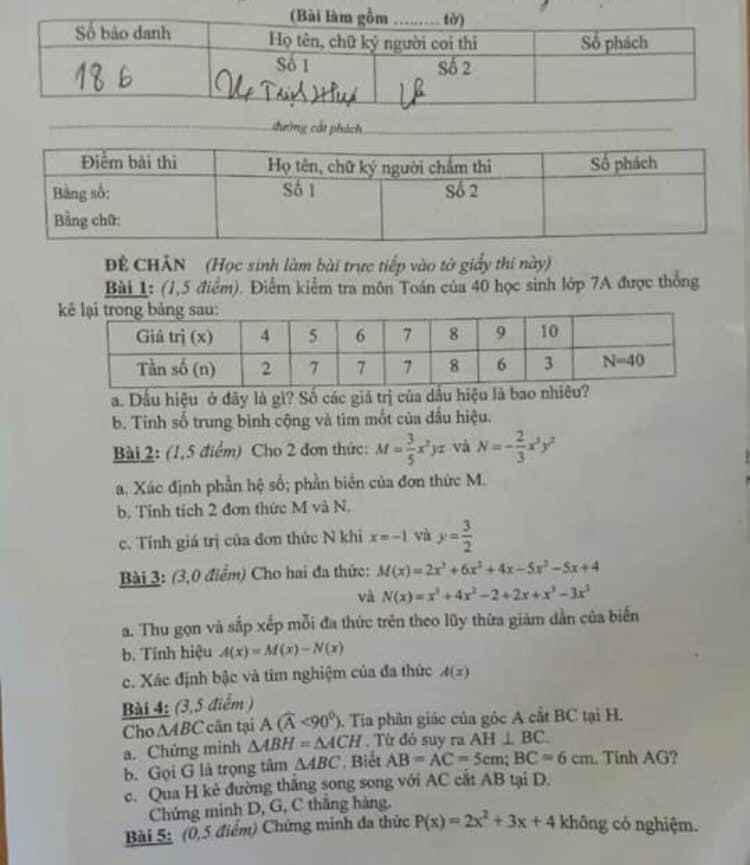 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 3 2022
Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
NK
2
Y
5 tháng 3 2023
\(a,\dfrac{4}{5}\times\dfrac{7}{3}\times\dfrac{3}{4}=\dfrac{4\times7\times3}{5\times3\times4}=\dfrac{7}{5}\)
\(b,\left(\dfrac{1}{2}+\dfrac{1}{3}\right)\times\dfrac{1}{4}\)
\(=\left(\dfrac{3}{6}+\dfrac{2}{6}\right)\times\dfrac{1}{4}\)
\(=\dfrac{5}{6}\times\dfrac{1}{4}\)
\(=\dfrac{5}{24}\)
\(c,\left(\dfrac{2}{3}+\dfrac{2}{5}\right)\times\dfrac{2}{7}\)
\(=\left(\dfrac{10}{35}+\dfrac{6}{35}\right)\times\dfrac{2}{7}\)
\(=\dfrac{16}{15}\times\dfrac{2}{7}\)
\(=\dfrac{32}{105}\)
C
5 tháng 3 2023
Cách `1`
`a)4/5 xx 7/3 xx 3/4`
`=28/15 xx 3/4`
`=84/60`
`=7/5`
__
`b)(1/2+1/3)xx1/4`
`=(3/6+2/6)xx1/4`
`=5/6xx1/4`
`=5/24`
__
`c)(2/3+2/5)xx2/7`
`=(10/15+6/15)xx2/7`
`=16/15xx2/7`
`=32/105`
___________________________
Cách `2`:
`a)4/5 xx 7/3 xx 3/4`
`=4/5 xx (7/3 xx 3/4)`
`=4/5 xx 7/4`
`=7/5`
__
`b)(1/2+1/3)xx1/4`
`=1/2 xx 1/4 + 1/3 xx 1/4`
`= 1/8 + 1/12`
`= 3/24+2/24`
`=5/24`
__
`c)(2/3+2/5)xx2/7`
`=2/3 xx 2/7 + 2/5 xx 2/7`
`=4/21 + 4/35`
`= 20/105+12/105`
`=32/105`
`#QiN`
MT
29 tháng 4 2021
Lề trái: cách mép trái từ 30 - 35 mm.
Lề phải: cách mép phải từ 15 - 20 mm.
Lề trên: cách mép trên từ 20 - 25 mm.
Lề dưới: cách mép dưới từ 20 - 25 mm.
PM
1
27 tháng 8 2021
a: Áp dụng định lí Pytago vào ΔBAC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+15^2=325\)
hay \(BC=5\sqrt{13}\left(cm\right)\)
Xét ΔBAC vuông tại A có
\(\sin\widehat{B}=\dfrac{AC}{BC}=\dfrac{15}{5\sqrt{13}}=\dfrac{3}{\sqrt{13}}\)
\(\Leftrightarrow\widehat{B}\simeq56^0\)
b: Xét ΔBAC có
BI là đường phân giác ứng với cạnh AC
nên \(\dfrac{AI}{AB}=\dfrac{CI}{BC}\)
hay \(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}\)
mà AI+CI=15cm
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AI}{10}=\dfrac{CI}{5\sqrt{13}}=\dfrac{AI+CI}{10+5\sqrt{13}}=\dfrac{15}{10+5\sqrt{13}}=\dfrac{-2+\sqrt{13}}{3}\)
Do đó: \(AI=\dfrac{-20+10\sqrt{13}}{3}\left(cm\right)\)
15 tháng 3 2019
Câu 26 trang 89 Sách Bài Tập (SBT) Toán Lớp 6 tập 2
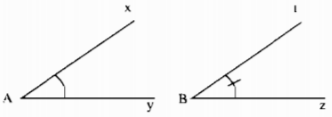
So sánh hai góc ở hình 10.
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi so sánh hai số đó
Cách 2: Vẽ lại hai góc lên giấy trong. Đặt chồng hai góc sao cho đỉnh trùng nhau, một cạnh trùng nhau, hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi vận dụng kiến thức bài 5 để kết luận.
Giải
Dùng thước đo độ để đo hai góc ở hình 10 và so sánh.
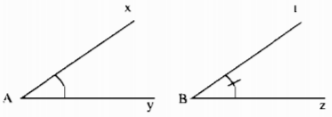
Tính tổng số đo hai góc trên hình 10.
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi cộng hai số đo.
Cách 2: Vẽ hai góc ở vị trí kề nhau rồi đo góc tổng.
Giải
Sử dụng thước đo độ sau đó cộng số đo hai góc.
a) Vẽ góc có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình.
b) Đóng hai chiếc đinh vào hai điểm A và B cách nhau 2,5 cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí \(M_1\). Đặt mẫu hình nhiều lần để được nhiều vị trí \(M_1,M_2,M_3\).. khác nhau của đỉnh M. Vậy ta có:
\(\widehat{AM_1B}=\widehat{AM_2B}=\widehat{AM_3B}=...=40^o\)
Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (hình 11)
Giải
b) Quỹ đạo của điểm M được gọi là "cung chứa góc \(40^o\)
Bài 29 tự làm,có trong sách mà bạn
15 tháng 3 2019
Bài 26 trang 89 Toán 6
So sánh hai góc ở hình 10.
Hướng dẫn: Cách 1: Đo riêng từng góc rồi so sánh hai số đó
Cách 2: Vẽ lại hai góc lên giấy trong. Đặt chồng hai góc sao cho đỉnh trùng nhau, một cạnh trùng nhau, hai cạnh còn lại của hai góc nằm cùng phía đối với cạnh trùng nhau rồi vận dụng kiến thức bài 5 để kết luận.
Giải: Dùng thước đo độ để đo hai góc ở hình 10 và so sánh.
Bài 27 trang 89
Tính tổng số đo hai góc trên hình 10.
Hướng dẫn:
Cách 1: Đo riêng từng góc rồi cộng hai số đo.
Cách 2: Vẽ hai góc ở vị trí kề nhau rồi đo góc tổng.
Giải: Sử dụng thước đo độ sau đó cộng số đo hai góc.
Bài 28 Toán 6
a) Vẽ góc có đỉnh là M trên giấy cứng. Cắt ra ta được một mẫu hình.
b) Đóng hai chiếc đinh vào hai điểm A và B cách nhau 2,5 cm. Đưa mẫu hình vào khe hở giữa hai chiếc đinh sao cho một cạnh sát A, một cạnh sát B. Khi đó đỉnh M của góc ở vị trí M1M1. Đặt mẫu hình nhiều lần để được nhiều vị trí M1,M2,M3M1,M2,M3, … khác nhau của đỉnh M. Vậy ta có:
ˆAM1B=ˆAM2B=ˆAM3B=…=400AM1B^=AM2B^=AM3B^=…=400
Đánh dấu khoảng 10 vị trí khác nhau của đỉnh M và dự đoán quỹ đạo của đỉnh M (hình 11)
HD: b) Quỹ đạo của điểm M được gọi là “cung chứa góc 400400.
29a) Ta có hình vẽ
b) Vì ˆARNARN^ và ˆSRNSRN^ kề bù nên:
ˆARN+ˆSRN=180OARN^+SRN^=180O
Thay ˆSRN=130OSRN^=130O ta có:
ˆARN+130O=180OARN^+130O=180O
⇒ˆARN=180O–130O=50O⇒ARN^=180O–130O=50O
Vì ˆARMARM^ và ˆMRSMRS^ kề bù nên:
ˆARM+ˆMRS=180OARM^+MRS^=180O
Thay ˆARM=130OARM^=130O ta có:
130O+ˆMRS=180O130O+MRS^=180O
⇒ˆMRS=180O–130O=50O⇒MRS^=180O–130O=50O
Vì hai tia RN và RM nằm trên cùng môt nửa mặt phẳng bờ chứa tia RA
ˆARN=50O;ˆARM=130OARN^=50O;ARM^=130O suy ra ˆARN<ˆARMARN^<ARM^
Nên tia RN nằm giữa hai tia RA và RM
⇒ˆARN+ˆMRN=ˆARM⇒ARN^+MRN^=ARM^. Thay ˆARN=50O;ˆARM=130OARN^=50O;ARM^=130O ta có:
50O+ˆMRN=130O50O+MRN^=130O
⇒ˆMRN=130O–50O=80O
15 tháng 6 2021
- Số tiền mua sách khuyến mãi là : \(\left(1-15\%\right).78,000=66300\) ( đồng )
- Số tiền mua truyện khuyến mãi là : \(\left(1-10\%\right).46,000=41,400\) ( đồng )
=> Tổng số tiền mua là : 66,300 + 41,400 = 107,700 ( đồng )
Vậy ...
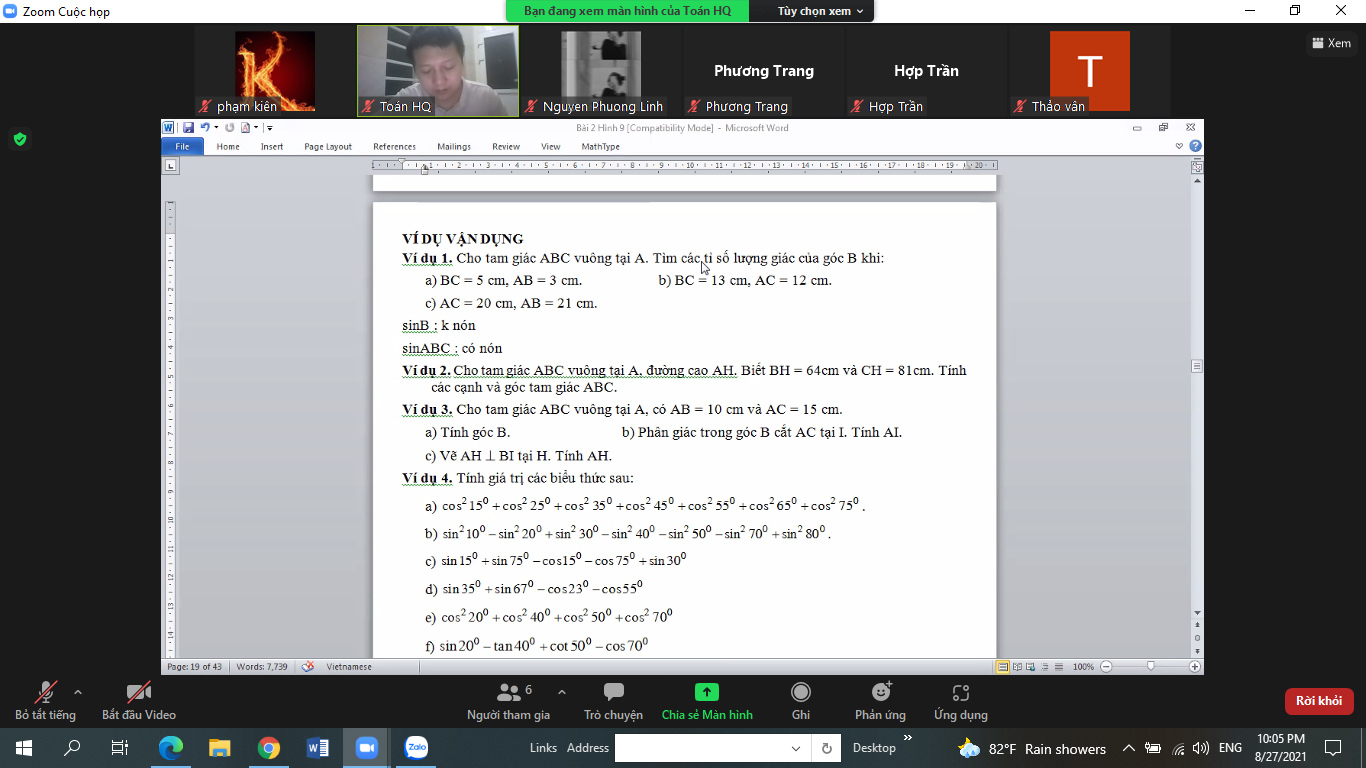
Bài 1:
a) Dấu hiệu: Điểm kiểm tra môn toán của 40 học sinh lớp 7A
số các giá trị: 40
b) số trung bình cộng: (4.2+5.7+6.7+7.7+8.8+9.6+10.3)/40=7,05
M0= 8