Cho hình chữ nhật ABCD có AB = 12cm, BC = 5cm. Chứng minh rằng bốn điểm A, B, C, D thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


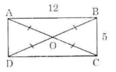
Gọi O là giao điểm của hai đường chéo AC và BD.
Ta có OA = OB = OC = OD (tính chất) nên bốn điểm A, B, C, D thuộc cùng một đường tròn (tâm O, bán kính OA)
Theo định lí Pitago trong tam giác vuông ABC có:
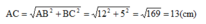
Nên bán kính đường tròn là OA = 13 : 2 = 6.5 cm

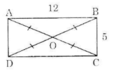
Gọi O là giao điểm của hai đường chéo AC và BD.
Ta có OA = OB = OC = OD (tính chất) nên bốn điểm A, B, C, D thuộc cùng một đường tròn (tâm O, bán kính OA)
Theo định lí Pitago trong tam giác vuông ABC có:
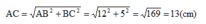
Nên bán kính đường tròn là OA = 13 : 2 = 6.5 cm

Gọi O là giao điểm hai đường chéo của hình chữ nhật, ta có OA=OB=OC=OD.
Bốn điểm A, B, C, D, cách đều điểm O nên bốn điểm này cùng thuộc một đường tròn.
Xét tam giác ABC vuông tại B, có AC^2=AB^2+BC^2=12^2+5^12=169 sUY RA AC = 13
Bán kính của đường tròn là R = 13 : 2 = 6,5
Nhận xét: Để chứng minh nhiều điểm cùng nằm trên một đường tròn, ta chứng minh các điểm này cùng cách đều một điểm.

Gọi O là giao điểm hai đường chéo của hình chữ nhật, ta có OA=OB=OC=OD.
Bốn điểm A, B, C, D, cách đều điểm O nên bốn điểm này cùng thuộc một đường tròn.
Xét tam giác ABC vuông tại B, có
Bán kính của đường tròn là
Nhận xét: Để chứng minh nhiều điểm cùng nằm trên một đường tròn, ta chứng minh các điểm này cùng cách đều một điểm.

a: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
nên ABCD là tứ giác nội tiếp
hay A,B,C,D thuộc 1 đường tròn
b: Gọi O là tâm đường tròn ngoại tiếp tứ giác ABCD
Suy ra: AC là đường kính của \(\left(O\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại B, ta được:
\(AC^2=AB^2+BC^2\)
\(\Leftrightarrow AC^2=12^2+5^2=169\)
hay AC=13cm
\(\Leftrightarrow OA=6.5\left(cm\right)\)

Xét tứ giác ABCD có
\(\widehat{A}+\widehat{C}=180^0\)
Do đó: ABCD là tứ giác nội tiếp
hay A,B,C,D cùng thuộc 1 đường tròn
Gọi R là bán kính của đường tròn ngoại tiếp hình chữ nhật ABCD
\(\Leftrightarrow R=\dfrac{AC}{2}=\dfrac{\sqrt{8^2+15^2}}{2}=\dfrac{17}{2}=8.5\left(cm\right)\)

Gọi O là giao điểm của hai đường chéo AC và BD.
Ta có OA = OB = OC = OD nên bốn điểm A, B,C,D thuộc cùng một đường tròn( tâm O, bán kính OA).
AC2 = AD2 + DC2 = 122 + 162 = 400
=> AC = 20
Bán kính của đường tròn bằng 10cm.
Gọi AC cắt BD ở E
Tứ giác ABCD là hcn , AC cắt BD ở E => EA=EB=EC=EC = AC/2
=> A,B,C,D thuộc đường tròn tâm E bán kính = AC/2
Xét tam giác ABC vuông tại b => AC^2=AB^2+BC^2 = 12^2+5^2=169
=> AC = 13 cm
=> Bán kính của đường tròn đó là AC/2 = 13/2 = 6,5 cm
Gọi O là giao điểm hai đường chéo của hình chữ nhật, ta có OA = OB = OC= OD.
Bốn điểm A, B, C, D, cách đều điểm O nên bốn điểm này cùng thuộc một đườngt ròn (tâm O, bán kính OA).
Xét tam giác ABC vuông tại B, có
AC2 = AB2 + BC2 = 122 + 52 = 169 ⇒ AC = \(\sqrt{169}\) = 13
Bán kính của đườngtròn là
OA = \(\frac{AC}{2}\) = \(\frac{13}{2}\) = 6,5 (cm)
Vậy bán kính đường tròn bằng 6,5 cm.