cho x,y>0 thay doi . tim GTNN cua
S=(X+Y)2/XY + (X+Y)2/(X2+Y2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LQ
1
LL
0
AH
Akai Haruma
Giáo viên
9 tháng 9 2018
Lời giải:
\(D=\frac{x}{y}+\frac{y}{x}+\frac{xy}{x^2+xy+y^2}=\frac{x^2+y^2}{xy}+\frac{xy}{x^2+xy+y^2}\)
\(=\frac{x^2+xy+y^2}{xy}+\frac{xy}{x^2+xy+y^2}-1\)
\(\frac{x^2+xy+y^2}{9xy}+\frac{xy}{x^2+xy+y^2}+\frac{8(x^2+xy+y^2)}{9xy}-1\)
Áp dụng BĐT Cô-si:
\(\frac{x^2+xy+y^2}{9xy}+\frac{xy}{x^2+xy+y^2}\geq 2\sqrt{\frac{x^2+xy+y^2}{9xy}.\frac{xy}{x^2+xy+y^2}}=\frac{2}{3}\)
\(x^2+y^2\geq 2xy\Rightarrow \frac{8(x^2+xy+y^2)}{9xy}\geq \frac{8.3xy}{9xy}=\frac{8}{3}\)
\(\Rightarrow D\geq \frac{2}{3}+\frac{8}{3}-1=\frac{7}{3}=D_{\min}\)
Dấu "=" xảy ra khi $x=y$
HT
3
24 tháng 1 2016
em xin lỗi chớ em mới lớp 6 thui anh Đức ạ
DT
0
CM
28 tháng 12 2019
Đáp án D
Phương pháp giải:
Đặt ẩn phụ, đưa về hàm một biến, dựa vào giả thiết để tìm điều kiện của biến
Lời giải:
Từ giả thiết chia cả 2 vế cho x2y2 ta được :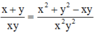 
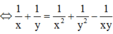
Đặt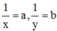 
ta có 
Khi đó 
Ta có 
mà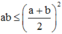 
nên 
Dấu đẳng thức xảy ra khi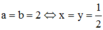 
. Vậy Mmax = 16
NT
0
VM
2
AH
Akai Haruma
Giáo viên
19 tháng 6 2021
Lời giải:
Áp dụng BĐT AM-GM:
$x^2+y^2\geq 2\sqrt{x^2y^2}=2|xy|\geq 2xy$
$\Rightarrow 3(x^2+y^2)\geq 6xy$
$x^2+9\geq 2\sqrt{9x^2}=2|3x|\geq 6x$
$y^2+9\geq 2\sqrt{9y^2}=2|3y|\geq 6y$
Cộng theo vế các BĐT trên:
$4(x^2+y^2)+18\geq 6(xy+x+y)=90$
$\Rightarrow x^2+y^2=18$
Vậy $A_{\min}=18$ khi $(x,y)=(3,3)$
AH
Akai Haruma
Giáo viên
20 tháng 6 2021
Sầu Riêng: của em nếu $x,y$ dương thì đúng. Còn trong bài $x,y$ thực thì đến đoạn $(x+y+2)^2\geq 64$ thì không khẳng định $x+y\geq 6$ được nha.
\(S=\frac{\left(x+y\right)^2}{xy}+\frac{\left(x+y\right)^2}{x^2+y^2}=\frac{x^2+y^2+2xy}{xy}+\frac{x^2+y^2+2xy}{x^2+y^2}=\frac{x^2+y^2}{xy}+\frac{2xy}{x^2+y^2}+3\)
\(=\frac{x^2+y^2}{2xy}+\frac{2xy}{x^2+y^2}+\frac{x^2+y^2}{2xy}+3\)
\(\ge2\sqrt{\frac{x^2+y^2}{2xy}.\frac{2xy}{x^2+y^2}}+\frac{2xy}{2xy}+3=6\)
Dấu "=" xảy ra khi x = y.
Vậy GTNN của S là 6.