cho đường tròn (O)có các dây AB và CD có AB>CD ,các tia AB và CD cắt nhau tại điểm M nằm bên ngoài dường tròn .gọi H và K theo thứ tự là trung điểm của AB và CD.So sánh độ dài MH và MK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 6 2017
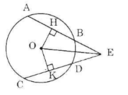
Nối OE ta có: AB = CD
=> OH = OK (Định lí 3)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
=> ΔOEH = ΔOEK (cạnh huyền, cạnh góc vuông)
=> EH = EK (1). (đpcm)
CM
17 tháng 2 2017
Ta có: OH ⊥ AB
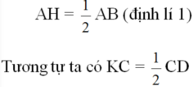
Mà AB = CD (gt) suy ra AH = KC (2)
Từ (1) và (2) suy ra:
EA = EH + HA = EK + KC = EC
Vậy EA = EC. (đpcm)
CM
18 tháng 9 2019
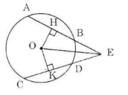
a) Nối OE ta có: AB = CD
=> OH = OK (Định lí 3)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
=> ΔOEH = ΔOEK (cạnh huyền, cạnh góc vuông)
=> EH = EK (1). (đpcm)
b) Ta có: OH ⊥ AB
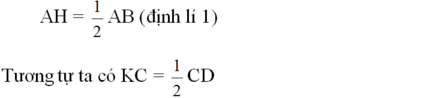
Mà AB = CD (gt) suy ra AH = KC (2)
Từ (1) và (2) suy ra:
EA = EH + HA = EK + KC = EC
Vậy EA = EC. (đpcm)
HH
15 tháng 7 2020
a) Nối OE ta có: AB = CD
=> OH = OK (Định lí 3)
Hai tam giác vuông OEH và OEK có:
OE là cạnh chung
OH = OK
=> \(\Delta OEH=\Delta OEK\)( cạnh huyền, cạnh góc vuông )
=> EH = EK (1). (đpcm)
b) Ta có: \(OH\perp AB\)
\(AH=\frac{1}{2}AB\left(đl1\right)\)
Tương tự , ta có : \(KC=\frac{1}{2}CD\)
Mà AB = CD (gt) suy ra AH = KC (2)
Từ (1) và (2) suy ra:
EA = EH + HA = EK + KC = EC
Vậy EA = EC (đpcm)
CM
10 tháng 6 2019
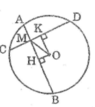
Ta có: HA = HB (gt)
Suy ra : OH ⊥ AB (đường kính dây cung)
Lại có : KC = KD (gt)
Suy ra : OK ⊥ CD (đường kính dây cung)
Mà AB > CD (gt)
Nên OK > OH (dây lớn hơn gần tâm hơn)
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
O M 2 = O H 2 + H M 2
Suy ra : H M 2 = O M 2 - O H 2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
O M 2 = O K 2 + K M 2
Suy ra: K M 2 = O M 2 - O K 2 (2)
Mà OH < OK (cmt) (3)
Từ (1), (2) và (3) suy ra: H M 2 > K M 2 hay HM > KM
25 tháng 4 2017
a)Vì HA=HB nên OH⊥AB
Vì KC=KD nên OK⊥CD
Mặt khác, AB=CD nên OH=OK (hai dây bằng nhau thì cách đều tâm).
ΔHOE=ΔKOE (cạnh huyền, cạnh góc vuông)
Suy ra EH=EK. (1)
b) Ta có AH=KC (một nửa của hai dây bằng nhau). (2)
Từ (1) và (2) suy ra EH+HA=EK+KC hay EA=EC.
27 tháng 9 2021
a, Ta có : d(O;AB) = OH
d(O;CD) = OK
AB = CD => OH = OK => EB = ED
mà H ; K lần lượt là trung điểm AB và CD => EH = EK
b, Vi OH = OK => AE = EC
Bài tập 13 trang 106 SGK Toán 9 Tập 1 - H7.net
Câu a: Ta có:
AH=HB⇒OH⊥ABAH=HB⇒OH⊥AB
KC=KD⇒OK⊥CDKC=KD⇒OK⊥CD
Lại có:
AB=CD⇒OH=OKAB=CD⇒OH=OK
⇒ΔHOE=ΔKOE(ch.cgv)⇒ΔHOE=ΔKOE(ch.cgv)
⇒EH=EK(1)⇒EH=EK(1)
Câu b: Ta lại có:
AB=CD⇔AB2=CD2⇔AH=CK(2)AB=CD⇔AB2=CD2⇔AH=CK(2)
Từ (1) và (2):
⇒EH+HA=EK+KC⇔EA=EC
a. Ta có: HA = HB ( gt )
Suy ra : \(OH\perp AB\) ( đường kính dây cung )
Lại có : KC = KD ( gt )
Suy ra : \(OK\perp CD\)( đường kính dây cung )
Mà AB > CD ( gt )
Nên OK > OH ( dây lớn hơn gần tâm hơn )
Áp dụng định lí Pitago vào tam giác vuông OHM ta có :
OM2 = OH2 + HM2
Suy ra : HM2 = OM2 – OH2 (1)
Áp dụng định lí Pitago vào tam giác vuông OKM ta có:
OM2 = OK2 + KM2
Suy ra: KM2 = OM2 – OK2 (2)
Mà OH < OK ( cmt ) (3)
Từ (1) (2) và (3) suy ra: HM2 > KM2 hay HM > KM