cho tam giác ABC, A=50 dộ.Tính góc B , góc C nếu
a) góc B= góc C
b) gócA = góc b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 6 2015
a, ĐÂy này
Tam giác ABC cân tại A
=> B = C = (180 - A ) / 2 = (180 - 70)/2 = 110/2 = 55độ
TAm giác CDH vuông tại H => C + CDH = 90độ
=> 55 + CDH = 90độ => CDH = 90 -55 = 35 độ
2 CDH = 2.35 = 70 độ = A
Cần ý B nhắn tin cho mình
AT
12 tháng 7 2021
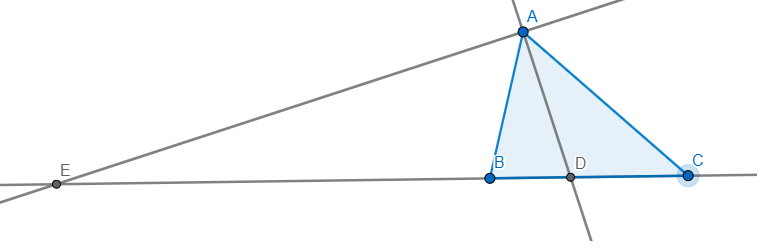
tia phân giác trong góc A cắt BC tại D
Vì AD,AE lần lượt là phân giác trong và ngoài của góc A \(\Rightarrow AD\bot AE\Rightarrow\angle EAB=90-\angle BAD=90-\dfrac{1}{2}\angle BAC\)
Ta có: \(\angle AEB=\angle ABC-\angle EAB=\angle ABC-90+\dfrac{1}{2}\angle BAC\)
\(=\angle ABC-90+\dfrac{1}{2}\left(180-\angle ABC-\angle ACB\right)\)
\(=\angle ABC-90+90-\dfrac{1}{2}\angle ABC-\dfrac{1}{2}\angle ACB=\dfrac{1}{2}ABC-\dfrac{1}{2}\angle ACB\)
S
2 tháng 9 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
1 tháng 8 2020
Bài giải : a) Ta có : góc XAB = ( góc ABC + góc ACB ) => 1/2 góc BAX = 1/2 ( góc ABC + góc ACB )
=> góc EAB = 1/2 ( góc B + góc C ) = B+ C/2 .
b) Ta có : góc B + góc C = 1800 - 600 = 1200 => góc EAB = 1/2.120 = 600. Xét tam giác AEC ta lại có : góc C = 1800 - góc EAC - góc AEC = 1800 - ( góc EAB + góc ABC ) - góc CEA = 1800 - ( 600 + 600 ) - 150 = 450. Xét tam giác ABC : góc A + góc B+ góc C = 1800
=> góc B = 1800 - góc A - góc C = 1800 - 600 -450 = 750 .
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180o
\(\widehat{B}+\widehat{C}\) = 180o - Â
\(\widehat{B}+\widehat{C}\) = 180o - 50o
\(\widehat{B}+\widehat{C}\) = 140o
a) \(\widehat{B}=\widehat{C}\) = 140o/2 = 70o
b) \(\widehat{A}=\widehat{B}=50^o\)
=> \(\widehat{A}+\widehat{B}\) = 50o.2 = 100o
=> \(\widehat{C}=\Delta ABC-\left(\widehat{A}+\widehat{B}\right)\)
\(\widehat{C}\) = 180o - 100o
\(\widehat{C}\) = 80o