Giải phương trình nghiệm nguyên:
x3 – y3 – 2y2 – 3y – 1 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có y = 0 không phải là nghiệm, còn y = -2 là nghiệm của BPT.

Ta có \(2y^2⋮2\Rightarrow x^2\equiv1\left(mod2\right)\Rightarrow x^2\equiv1\left(mod4\right)\Rightarrow2y^2⋮4\Rightarrow y⋮2\Rightarrow x^2\equiv5\left(mod8\right)\) (vô lí).
Vậy pt vô nghiệm nguyên.
2: \(PT\Leftrightarrow3x^3+6x^2-12x+8=0\Leftrightarrow4x^3=\left(x-2\right)^3\Leftrightarrow\sqrt[3]{4}x=x-2\Leftrightarrow x=\dfrac{-2}{\sqrt[3]{4}-1}\).

Lời giải:
PT $\Leftrightarrow 3x^2+x(5y-8)-(2y^2+9y+4)=0$
Coi đây là pt bậc 2 ẩn $x$. Để pt có nghiệm nguyên thì:
$\Delta=(5y-8)^2+12(2y^2+9y+4)=t^2$ với $t\in\mathbb{N}$)
$\Leftrightarrow 49y^2+28y+112=t^2$
$\Leftrightarrow (7y+2)^2+108=t^2$
$\Leftrightarrow 108=(t-7y-2)(t+7y+2)$
Đến đây là dạng phương trình tích đơn giản rồi. Bạn chỉ cần xét TH. Lưu ý rằng $t+7y+2>0$ và $t-7y-2, t+7y+2$ có cùng tính chẵn lẻ.


Ta có
2 x + 3 y = 7 2 − m 4 x − y = 5 m ⇔ 4 x + 6 y = 7 − 2 m 4 x − y = 5 m ⇔ 7 y = 7 − 7 m 4 x − y = 5 m ⇔ y = 1 − m 4 x − 1 − m = 5 m ⇔ y = 1 − m x = 4 m + 1 4
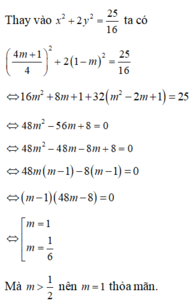
Đáp án: B

Với câu a)bạn nhân cả 2 vế cho 12 rồi ép vào dạng bình phương 3 số
Câu b)bạn nhân cho 8 mỗi vế rồi ép vào bình phương 3 số
Ta có x³- y³ - 2y² - 3y - 1= 0
Hay x³ = y³ + 2y² + 3y + 1 bạn sử dụng pp đánh giá
Do y² ≥ 0 nên y³ - 3y² + 3y - 1 < y³ + 2y² + 3y + 1
và y³ + 2y² + 3y + 1 ≤ y³ + 3y² + 3y + 1
( y - 1 )³ < x³ ≤ ( y + 1 )³
Nếu x³ = y³ tìm được nghiệm ( -1; -1 )
Nếu x³ = ( y + 1 )³ tìm được nghiệm ( 1; 0 )