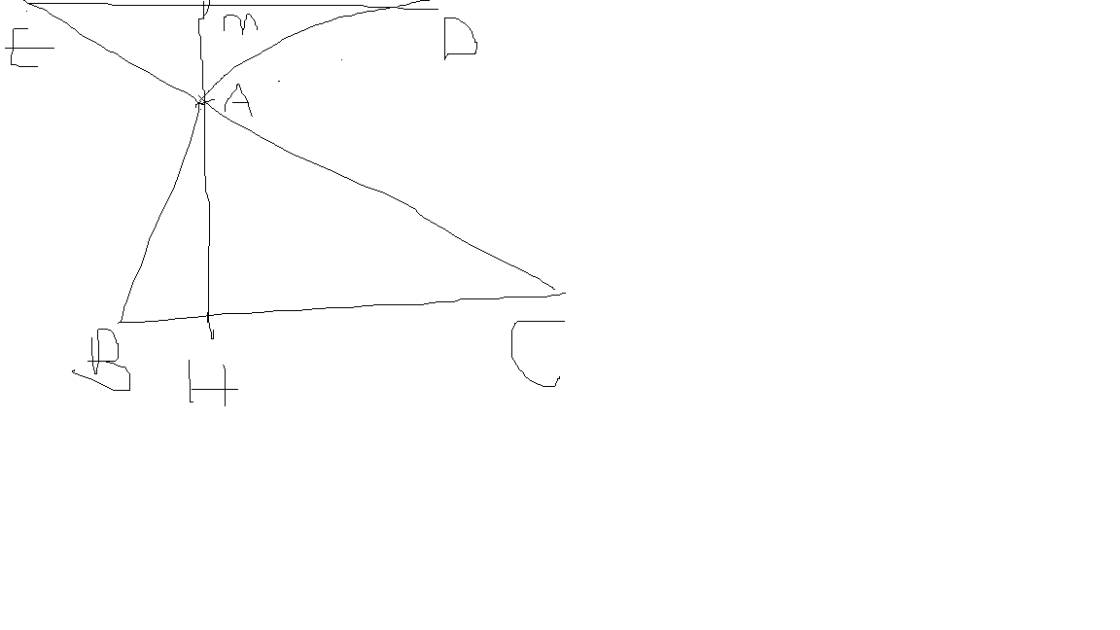
Cho tam giác ABC nhọn. Trung tuyến AM. Trên nửa mặt phẳng bờ AC ko chứa B, vẽ tia Ay vuông góc với AC. Trên nửa mặt phẳng bờ AB ko chứa C, vẽ tia Ax vuông góc với AB.Trên tia Ax lấy điểm E sao cho AE=AB. Trên tia Ay lấy điểm F sao cho AF=AC. Tính tỉ số \(\frac{AM}{EF}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 2 2021
a) Xét ΔKIM và ΔAIN có
KI=AI(I là trung điểm của KA)
\(\widehat{KIM}=\widehat{AIN}\)(hai góc đối đỉnh)
IM=IN(I là trung điểm của MN)
Do đó: ΔKIM=ΔAIN(c-g-c)
nên MK=AN(hai cạnh tương ứng)
mà AN=AC(gt)
nên MK=AC(đpcm)
BT
8 tháng 12 2017
Lấy điểm M thuộc tia AM sao cho M là trung điểm của AM.
Ta chứng minh được:
\(\Delta AMB=\Delta M'MC\left(c.g.c\right)\) suy ra AB = BM'.
\(\Delta AMC=\Delta M'MB\left(c.g.c\right)\Rightarrow AC=BM'\), \(\widehat{CAM}=\widehat{BM'M}\).
Theo định lý tổng ba góc trong tam giác:
\(\widehat{M'AB}+\widehat{BM'A}+\widehat{ABM'}=180^o\Leftrightarrow\widehat{BAM'}+\widehat{ABM'}+\widehat{M'AC}=180^o\).
Mà \(\widehat{DAE}+\widehat{BAM}+\widehat{MAC}=180^o\).
Suy ra \(\widehat{DAE}=\widehat{ABM'}\).
Xét tam giác DAE và tam giác ABM' cóL
DA = AB.
BM' = AC = AE.
\(\widehat{DAE}=\widehat{ABM'}\).
Suy ra \(\Delta DAE=\Delta AB'M\left(c.g.c\right)\).
Suy ra DM = AM' = 2AM. (đpcm).
