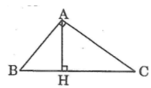
Cho tam giác ABC nhon, đường cao AH. Chứng minh rằng AB×SinB=AC×SinC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 9 2017
Ta có AB^2+AC^2=10^2+24^2=676
BC^2=26^2=676
=> Tam Giác ABC vuông tại A(đpcm)
b, \(\sin B=\frac{AC}{BC}=\frac{24}{26}=\frac{12}{13}\)
\(\sin C=\frac{AB}{BC}=\frac{10}{26}=\frac{5}{13}\)
c,Áp dụng hệ thức AB.AC=AH.BC
=> AH=AB.AC/BC=10.24/26=9,2
\(AB^2=BH.BC\)\(\Leftrightarrow10^2=BH.26\)\(\Rightarrow BH\approx3,8\)
\(\Rightarrow CH=22,2\)
12 tháng 9 2017
Câu a :
Ta có :
\(21^2+28^2=35^2\) ( py - ta - go )
\(\Rightarrow ABC\) vuông tại A .
Câu b :
\(sinB=\dfrac{AC}{BC}=\dfrac{28}{35}=\dfrac{4}{5}=0^048^'0^"\)
\(\sin C=\dfrac{AB}{BC}=\dfrac{25}{35}=\dfrac{5}{7}=0^042^'51,43^"\)
27 tháng 7 2018
Bài 1 :
Câu a : Theo định lý py-ta-go cho \(\Delta AHB\) ta có :
\(AH=\sqrt{AB^2-BH^2}=\sqrt{13^2-5^2}=12cm\)
\(\Rightarrow\sin B=\dfrac{AH}{AB}=\dfrac{12}{13}\approx0,92\)
Theo hệ thức lượng cho \(\Delta ABC\) ta có :
\(AH^2=BH.HC\Leftrightarrow HC=\dfrac{AH^2}{BH}=\dfrac{12^2}{5}=28,8cm\)
Theo định lý py - ta - go cho \(\Delta AHC\) ta có :
\(AC=\sqrt{AH^2+HC^2}=\sqrt{12^2+28,8^2}=31,2cm\)
\(\Rightarrow\sin C=\dfrac{AH}{AC}=\dfrac{12}{31,2}\approx0,38\)
Câu b tương tự !
Chúc bạn học tốt
13 tháng 8 2017
a)Kẻ đường cao : BH , AI , CK
Ta có: sinA = BH / c ; sinB = AI / c
=> sinA/sinB = BH / AI ﴾1﴿
Mà BH = a.sinC ; AI = b.sinC
=> BH/AI = a/b ﴾2﴿
Từ ﴾1﴿ và ﴾2﴿ suy ra sinA/sinB = a/b => a/sinA = b/sinB
Bạn chỉ việc nói chứng minh tượng tự , ta có:
b/sinB = c/sinC ; c/sinC = a/sinA
Từ đó suy ra a /sinA = b / sinB = c /sinC
Chúc bạn học tốt
NHỚ TK MK NHA
TN
0
