rút gọn :
a, 1 + 2 + 22 + ... + 2100
b, 1 + 3 + 32 + ... + 3100
c, 1 + 4 + 42 + ... + 4100
d, 1 + 10 + 102 + ... + 10100
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
22 tháng 6 2023
\(A=\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{99}}\)
\(\Rightarrow\dfrac{A}{3}=\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\)
\(\Rightarrow A-\dfrac{A}{3}=\dfrac{2A}{3}=\left(\dfrac{1}{3}+\dfrac{1}{3^2}+\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\right)-\left(\dfrac{1}{3^2}+\dfrac{1}{3^3}+\dfrac{1}{3^4}+...+\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\dfrac{2A}{3}=\left(\dfrac{1}{3^2}-\dfrac{1}{3^2}\right)+\left(\dfrac{1}{3^3}-\dfrac{1}{3^3}\right)+...+\left(\dfrac{1}{3^{99}}-\dfrac{1}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)=\dfrac{1}{3}-\dfrac{1}{3^{100}}\)
\(\Rightarrow2A=3\cdot\left(\dfrac{1}{3}-\dfrac{1}{3^{100}}\right)\)
\(\Rightarrow\text{A}=\dfrac{1-\dfrac{1}{3^{99}}}{2}\)
\(\Rightarrow A=\dfrac{1}{2}-\dfrac{1}{2.3^{99}}< \dfrac{1}{2}\)
NL
2
21 tháng 8 2021
a: Ta có: \(A=2+2^2+2^3+2^4+...+2^{100}\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{99}\left(1+2\right)\)
\(=3\cdot\left(2+2^3+...+2^{99}\right)⋮3\)
b: Ta có: \(B=4+4^2+4^3+...+4^{2022}\)
\(=4\left(1+4\right)+4^3\left(1+4\right)+...+4^{2021}\left(1+4\right)\)
\(=5\cdot\left(4+4^3+...+4^{2021}\right)⋮5\)
TB
2
6 tháng 3 2023
Ta thấy \(\dfrac{1}{2^2}< \dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2.3}\)
......
\(\dfrac{1}{10^2}< \dfrac{1}{9.10}\)
hay \(D=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+....+\dfrac{1}{10^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\)
\(D< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+....+\dfrac{1}{9}-\dfrac{1}{10}\)
\(D< 1-\dfrac{1}{10}=\dfrac{9}{10}< 1\) ( đpcm )
6 tháng 3 2023
Ta có \(\dfrac{1}{2.2}\) < \(\dfrac{1}{1.2}\)
\(\dfrac{1}{3.3}\)<\(\dfrac{1}{2.3}\)
\(\dfrac{1}{4.4}\)<\(\dfrac{1}{3.4}\)
.........................
\(\dfrac{1}{10.10}\)<\(\dfrac{1}{9.10}\)
=>\(\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{10.10}\)\(< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{9.10}\)
=> D < 1 - \(\dfrac{1}{10}\)
=>D < \(\dfrac{9}{10}\)
=> D < \(\dfrac{10}{10}\)
Vậy D < 1
NT
2
NT
27 tháng 4 2021
a.Chứng tỏ rằng B = 1/22 + 1/32 + 1/42 + 1/52 + 1/62 + 1/72 +1/82 < 1
b.Cho S = 3/1.4 + 3/4.7 + 3/7.10 +......+3/40.43 + 3/43.46 hãy chứng tỏ rằng S < 1
NT
27 tháng 4 2021
Xin lỗi mọi người mình tính đặt câu hỏi nhưng ấn nhầm phần trả lời ạ!
NT
0
7 tháng 3 2018
1,
a,-3/5
b,-1/2
c,19/39
d,1/4
e,-39/40
f,-59/56
2,
a,=
b,<
c,>
d,<
k cho mình nha
CM
15 tháng 7 2019
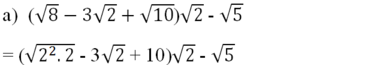
= (2√2 - 3√2 + 10)√2 - √5
= 2.(√2)2 - 3.(√2)2 + √10.√2 - √5
= 4 - 6 + √20 - √5 = -2 + 2√5 - √5
= -2 + √5
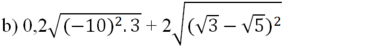
= 0,2.10.√3 + 2|√3 - √5|
s
= 2√3 + 2(√5 - √3)
= 2√3 + 2√5 - 2√3 = 2√5
PT
1
25 tháng 7 2018
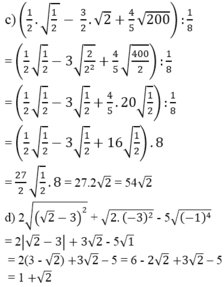
12/18 + 12/42 = 2/3 + 2/7 = 14/21 + 6/21 = 20/21
1/2 + 2/4 + 3/6 + 4/8 + 5/10 + 6/12
= 1/2 + 1/2 + 1/2 + 1/2 + 1/2 + 1/2
= 1/2 x 6
=6/2
=3
a/ta gọi biểu thức trên là A.
ta có: A=1+2+22+...+2100
2A= 2x(1+2+22+...+2100)
2A= 2x1+2x2+22x2+...+2100x2
2A= 2+22+23+....+2101
2A-A=A=(2+22+23+....+2101)-(1+2+22+...+2100)
A= 2101-1
b/ làm tương tụ như câu a nhưng cuối cùng phải thêm '':2'' (vì lúc đó ta tính ra 3A - A =2A nên phải chia 2)