cho hình bình hành ABCD gọi E,F theo thứ tự là trung điểm của AB,CD Gọi M là giao điểm của AF và DE, N là giao điểm BF và CE
a) CMR EMFN là hình bình hành
b) Các Đường thẳng AC, EF, MN Đồng quy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LH
18 tháng 9 2016
làm đc mỗi câu b :))
AEFC là hình bình hành ( tự cm nhá :) )
=> đường chéo AC giao đường chéo EF tại trung điểm của EF
câu a => đường chéo MN giao đường chéo EF tại trung điểm của EF
=> ĐPCM
câu b thui, câu a lằng nhằng quá lười nghĩ thông cảm nhé
N
18 tháng 9 2019
a.
Xet 2 tam giac ADE va CBF ta co:
\(\widehat{A}=\widehat{C}\)(2 goc doi cua hinh binh hanh)
\(AE=CF\)
\(AD=BC\)(2 canh doi cua hinh binh hanh)
Do do:\(\Delta ADE=\Delta CBF\left(c-g-c\right)\)
Suy ra:\(DE=BF\)(2 canh tuong ung)
b.Xet 2 tam giac ADF va CBE ta co:
\(\widehat{D}=\widehat{B}\)(2 goc doi cua hinh binh hanh)
\(DF=BE\)
\(AD=CB\)(2 canh doi cua hinh binh hanh)
Do do:\(\Delta ADF=\Delta CBE\left(c-g-c\right)\)
Suy ra:\(AF=CE\)(2 canh tuong ung)
Tu giac AECF co:
\(AE=CF\)
\(AF=CE\)
Nen AECF la hinh binh hanh
Suy ra:\(\widehat{BAF}=\widehat{DCE}\)(2 goc doi cua hinh binh hanh)
Theo chung minh o cau a ta co:\(\Delta ADE=\Delta CBF\)
Suy ra:\(\widehat{AED}=\widehat{CFB}\)(2 goc tuong ung)
Xet 2 tam giac EAM va FCN ta co:
\(AE=CF\)
\(\widehat{BAF}=\widehat{DCE}\)
\(\widehat{AED}=\widehat{CFB}\)
Do do:\(\Delta EAM=\Delta FCN\left(g-c-g\right)\)
Suy ra:\(EM=FN\left(1\right)\)(2 canh tuong ung)
Va \(\widehat{AME}=\widehat{CNF}\)(2 goc tuong ung)
Ma \(\widehat{DMF}=\widehat{AME}\left(2\right)\)
\(\widehat{BNE}=\widehat{CNF}\left(3\right)\)
Tu (2) va (3) suy ra:\(\widehat{DMF}=\widehat{BNE}\)
Tu giac EBFD co:
\(BE=DF\)
\(DE=BF\)(chung minh o cau a)
Nen EBFD la hinh binh hanh
Suy ra;\(\widehat{EDF}=\widehat{FBE}\)(2 goc doi cua hinh binh hanh)
Xet 2 tam giac DMF va BNE ta co:
\(\widehat{DMF}=\widehat{BNE}\)
\(\widehat{EDF}=\widehat{FBE}\)
\(DF=BE\)
Do do:\(\Delta DMF=\Delta BNE\left(c-g-c\right)\)
Suy ra;\(MF=NE\left(4\right)\)(2 canh tuong ung)
Tu (1) va (4) suy ra:EMFN la hinh binh hanh
CM
13 tháng 12 2017
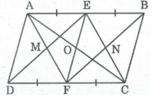
Gọi O là giao điểm của AC và EF
Tứ giác AECF là hình bình hành ⇒ OE = OF
Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Suy ra: MN đi qua trung điểm O của EF.
Vậy AC, EF, MN đồng quy tại O.
