Cho tam giác ABC vuông tại A , đường cao Ah .Biết HB = 25 cm, hc=64 cm .Tính góc B và góc C cua tam giác trên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 10 2017
Đáp án C
Ta có: BC = HB + HC = 25 + 64 = 89 cm
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
NN
1
AH
Akai Haruma
Giáo viên
29 tháng 12 2022
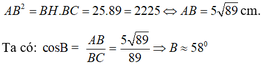
Lời giải:
$BC=BH+CH=25+64=89$ (cm)
Áp dụng công thức hệ thức lượng trong tam giác vuông:
$AH^2=BH.CH=25.64\Rightarrow AH=40$ (cm)
Diện tích tam giác $ABC$ là: $AH.BC:2=40.89:2=1780$ (cm2)
16 tháng 5 2022
\(AH=\sqrt{25\cdot64}=40\left(cm\right)\)
Xét ΔAHB vuông tại H có
\(\tan B=\dfrac{AH}{HB}=\dfrac{40}{25}=1.6\)
nên \(\widehat{B}\simeq58^0\)
hay \(\widehat{C}=32^0\)
13 tháng 5 2021
b) ΔAHB vuông tại H
Áp dụng định lý Pi-ta-go ta có: AH2+ BH2= AB2
⇒ 42 + 22 = AB2
⇒AB2 = 20
⇒AB = √20
ΔAHC vuông tại H
Áp dụng định lý Pi-ta-go, ta có: AH2 + HC2 = AC2
⇒42 +82 = AC2
⇒ AC2 = 80
⇒AC = √80
b)Vì AB>AC(√20>√80)
⇒góc C lớn hơn góc B (quan hệ giữa góc và cạnh đối diện)
CH
Cô Hoàng Huyền
Admin
VIP
18 tháng 5 2016
Cô hướng dẫn nhé :)
a. \(\Delta ABH=\Delta ADH\) (Hai cạnh góc vuông)
b. Ta thấy góc CDE = góc HDA (đối đỉnh) \(\Rightarrow\) góc DEC = góc HAD (Cùng phụ với hai góc bên trên)
Lại do câu a có \(\Delta ABH=\Delta ADH\) nên góc DAH = góc HAB. Mà góc HAB = góc HCA.
Vậy góc ECD = góc DCA
c. Xét tam giác ACM có CH vừa là đường cao, vừa là phân giác nên tam giác ACM cân tại C.
Chúc em học tốt ^^
18 tháng 5 2016
cô ơi sao góc DEC là góc vuông còn góc HAD là góc nhọn sao bằng nhau được ạ
26 tháng 7 2018
a.Áp dụng hệ thức h^2=b'.c' vào tam giác vuông ABC ta có: AH^2=HB.HC(đpcm)
AH^2=HB.HC suy ra AH^2=1,8.3,2 suy ra AH^2=5,76 suy ra AH=2,4
S tam giác ABC=1/2 AH.(HB+HC)=1/2.2,4.5=6
