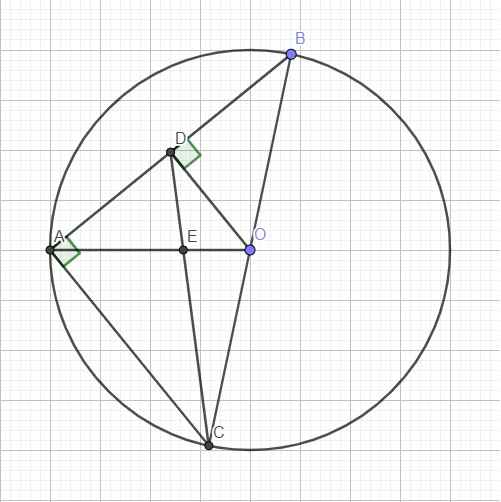
Cho góc nhọn xOy cắt đường tròn tâm O bán kính r tại A và B . Gọi I là trung điểm của đoạn thẳng AB . Chứng minh rằng OI vuông góc với AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 10 2021
a: Xét (O) có
ΔBNC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBNC vuông tại N
Xét (O) có
ΔBMC nội tiếp đường tròn
BC là đường kính
Do đó: ΔBMC vuông tại M
Xét ΔABC có
BN là đường cao
CM là đường cao
BN cắt CM tại H
Do đó: AH\(\perp\)BC
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 7 2021
\(\widehat{BAC}\) là góc nội tiếp, mà \(\widehat{BAC}=90^0\Rightarrow\widehat{BAC}\) là góc nội tiếp chắn nửa đường tròn
\(\Rightarrow BC\) là đường kính \(\Rightarrow\) O là trung điểm BC
\(\Rightarrow B,O,C\) thẳng hàng
b.
Do D là trung điểm AB \(\Rightarrow OD\perp AB\Rightarrow OD||AC\) (cùng vuông góc AB)
Mà O là trung điểm BC, D là trung điểm AB
\(\Rightarrow\) OD là đường trung bình tam giác ABC
\(\Rightarrow OD=\dfrac{1}{2}BC\)
Nối AO cắt CD tại E
Áp dụng định lý talet: \(\dfrac{OE}{EA}=\dfrac{OD}{AC}=\dfrac{1}{2}\Rightarrow OE=\dfrac{1}{2}EA\Rightarrow OE=\dfrac{1}{3}OA\)
Do O cố định, A cố định \(\Rightarrow\) E cố định
\(\Rightarrow\) CD luôn đi qua điểm E cố định
