trên quãng sông AB dài 56 km một canô xuôi từ A đến B rồi quay trở lại và đỗ tại một địa điểm C mà AC=3BC , thời gian ca nô xuôi dòng và ngược lại hết 3 giờ 6 phút . Tính vận tốc riêng của ca nô biết rằng một đám bèo tây thả trôi trên sông đó , 15 phút trôi được 750m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 4 2023
Vận tốc khi xuôi dòng của ca nô là: 25 + 5 = 30 (km/h)
Thời gian ca nô xuôi dòng từ A đến B là: 72 : 30 = 2,4 ( giờ)
Vận tốc ca nô khi ngược dòng là: 25 - 5 = 20 (km/h)
Thời gian ca nô ngược dòng từ B đến A là:
72 : 20 = 3,6 giờ
Đổi 2,4 giờ = 2 giờ 24 phút; 3,6 giờ = 3 giờ 36 phút
Ca nô về tới A lúc:
5 giờ + 2 giờ 24 phút + 3 giờ 36 phút + 80 phút = 12 giờ 20 phút
Đáp số: 12 giờ 20 phút
2 tháng 3 2019
Gọi vận tốc riêng của canoo là x ( x>0
vận tốc cano đi xuôi là x + 4 (km/h)
thời gian cano đi xuôi là : \(\frac{80}{x+4}\)km/ h
vận tốc cano đi ngc là ; x - 4 (km/h)
thời gian cano đi ngc hết là \(\frac{72}{x-4}\)
ta lại có thời gian khi đi xuôi ít hơn thời gian đi ngc là 15 ph= \(\frac{1}{4}\)h
\(\Rightarrow\)pt \(\frac{80}{x+4}\)+\(\frac{1}{4}\)=\(\frac{72}{x-4}\)
giải ra ta đc x = 36
TC
23 tháng 2 2020
Đổi 15p = \(\frac{1}{4}\)h
Gọi vận tốc ca nô khi dòng nước yên lặng là x (km/h) ĐK: x > 0
Vận tốc của ca nô khi xuôi dòng: x + 4 (km/h)
Vận tốc của ca nô khi ngược dòng: x - 4 (km/h)
Thời gian ca nô xuôi dòng : \(\frac{80}{x+4}\)(h)
Thời gian ca nô ngược dòng : \(\frac{72}{x-4}\)(h)
Ta có PT: \(\frac{72}{x-4}-\frac{80}{x+4}=\frac{1}{4}\)
\(\Leftrightarrow\frac{288\left(x+4\right)-320\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}=\frac{x^2-16}{\left(x+4\right)\left(x-4\right)}\)
\(\Leftrightarrow x^2+32x-2448=0\)
Giai PT ta được x1 = 36 (Nhận)
x2 = -68 (Loại)
Vậy vận tốc thực của ca nô là 36km/h
CM
16 tháng 2 2017
15 phút = (1/4)giờ
Gọi vận tốc của ca nô khi nước đứng yên là x (km/h). Điều kiện x > 2
Vận tốc ca nô khi xuôi dòng là x + 2 (km/h)
Vận tốc ca nô khi ngược dòng là x – 2 (km/h)
Thời gian ca nô khi xuôi dòng là:
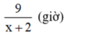
Thời gian ca nô khi ngược dòng là:
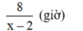
Ta có phương trình:
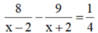
Quy đồng mẫu hai vế:
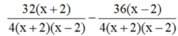
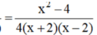
Suy ra:
32x + 64 - 36x + 72 = x2 - 4
⇔ -4x + 136 = x2 - 4
⇔ x2 + 4x - 140 = 0
⇔ (x2 + 4x + 4) - 144 = 0
⇔ (x + 2)2 - 122 = 0
⇔ (x + 14)(x - 10) = 0
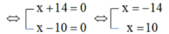
Giá trị x = -14 không thỏa mãn điều kiện
Giá trị x = 10 thỏa mãn điều kiện
Vậy vận tốc của ca nô khi nước yên lặng là 10km/h
25 tháng 2 2023
a: Gọi vận tốc thật của cano là x
Theo đề, ta có: 48/x-2-48/x+2=2/5
=>24/x-2-24/x+2=1/5
=>5[24(x+2)-24(x-2)]=(x+2)(x-2)
=>x^2-4=5(24x+48-24x+48)
=>x^2-4=5*96=480
=>x^2-484=0
=>x=22
b: Thời gian đi từ A đến B là 48/22-2=48/20=2,4(h)
=>Lúc tới B đã 6h15'+2h24'=8h39'
=>Lúc đi từ B về A thì đã 8h39'+20'=8h59'
Thời gian đi từ B về A là 48/22+2=2(h)
=>Khi về tới A đã là: 8h59'+2h=10h59'
20 tháng 1 2016
Gọi vận tốc riêng ca nô là x ; vận tốc nước là y
=> xuôi dòng là x + y ; ngược dòng là x - y
HPT :
\(\int^{\frac{100}{x+y}+\frac{100}{x-y}=15}_{\frac{50}{y}=\frac{100}{x+y}+\frac{50}{x-y}}\)
DD
Đoàn Đức Hà
Giáo viên
6 tháng 7 2021
Vận tốc của cano khi đi xuôi dòng là:
\(25+5=30\left(km/h\right)\)
Thời gian cano đi từ A đến B là:
\(72\div30=2,4\left(h\right)\)
Vận tốc của cano khi đi ngược dòng là:
\(25-5=20\left(km/h\right)\)
Thời gian cano đi từ B về A là:
\(72\div20=3,6\left(h\right)\)
Đổi: \(2,4h=2h24';3,6h=3h36'\)
Cano về tới A lúc:
\(5h+2h24'+80'+3h36'=12h20'\)
18 tháng 8 2021
Từ A đến B:
vận tốc của cano: v = 25 + 5 =30(km/h)
Thời gian: t =svsv
= 72/30= 2.4h= 2h24'
Từ B đến A
vận tốc của cano: v = 25 - 5 =20(km/h)
Thời gian: t =svsv
= 72/0= 3.6h= 3h36'
Vậy thời gian cần tìm : 2h24' + 3h36' + 80' = 7h20'
:3
