GIẢI THÍCH VÌ SAO CÁC PHÂN SỐ SAU VIẾT ĐƯỢC DƯỚI DẠNG SỐ THẬP PHÂN HỮU HẠN RỒI VIẾT CHÚNG DƯỚI DẠNG ĐÓ
\(\frac{3}{8}\); \(\frac{-7}{5}\)
\(\frac{13}{20}\);\(\frac{-13}{125}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 8 2016
- \(\frac{3}{8}\) đc viết dưới dạng số thập phân hữu hạn vì có mẫu là 8 = 23 (ko có ước nguyên tố khác 2 và 5)
- \(\frac{-7}{5}\) đc viết dưới dạng số thập phân hữu hạn vì có mẫu là 5 = 5 (ko có ước nguyên tố khác 2 và 5)
- \(\frac{13}{20}\) đc viết dưới dạng số thập phân hữu hạn vì có mẫu là 20 = 22.5 (ko có ước nguyên tố khác 2 và 5)
\(\frac{-13}{125}\) đc viết dưới dạng số thập phân hữu hạn vì có mẫu là 125 = 53 (ko có ước nguyên tố khác 2 và 5)
Tick cho mình với nha!!!!!!!!
31 tháng 10 2021
Vì khi phân tích mẫu ra thừa số nguyên tố thì không có thừa số nào khác 2 và 5, nên cả bốn phân số này được viết dưới dạng số thập phân hữu hạn
CM
5 tháng 3 2019
Ta có: 16 = 24
125 = 53
40 = 23. 5
25 = 52
Các phân số:
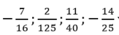
viết được dưới dạng số thập phân hữu hạn vì mẫu số của chúng chỉ có thừa số nguyên tố 2 và 5
11 tháng 10 2015
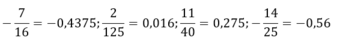
vì 8=2^2.3
5=5
20=2^2.5
125=5^3
đúng nhé nhưng cậu phải trình bày đầy đủ
CM
22 tháng 8 2019
+ 8 = 23 chỉ có ước nguyên tố là 2
⇒ 
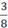viết được dưới dạng số thập phân hữu hạn. 
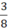= 0,375
+ 5 chỉ có ước nguyên tố là 5
⇒ 
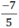viết được dưới dạng số thập phân hữu hạn. 
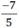= -1,4
+ 20 = 22.5 có ước nguyên tố là 2 và 5.
⇒ 
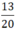viết được dưới dạng số thập phân hữu hạn. 
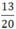= 0,65
+ 125 = 53 chỉ có ước nguyên tố là 5.
⇒ 
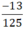viết được dưới dạng số thập phân hữu hạn. 
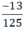= -0,104
Các phân số đã cho có mẫu dương và các mẫu đó lần lượt là 8 = 23 , 5, 20 = 22. 5 , 125 = 53 đều không chứa thừa số nguyên tố nào khác 2 và 5 nên chúng được viết dưới dạng số thập phân hữu hạn
Ta được;
\(\frac{3}{8}\)= 0,375 ; \(\frac{-7}{5}\)= −1,4 ; \(\frac{13}{20}\)= 0,65 ; \(\frac{-13}{125}\) =0,104
\(\frac{3}{8}=0,375\)( vì 8 = 23 )
\(\frac{-7}{5}=-1,4\)( vì mẫu có 5 )
\(\frac{13}{20}=0,65\)( vì 20 = 22 . 5 )
\(\frac{-13}{125}=-0,104\)( vì 125 = 53 )
- Quy tắc : nếu dưới mẫu chỉ có ước nguyên tố là 2 và 5 hoặc riêng 2 , 5 , không có ước nguyên tố khác 2 và 5 thì viết được dưới dạng số thập phân hữu hạn