Cho nửa đường tròn có đường kính AB=2R. Vẽ các tiếp tuyến Ax, By với nửa đường tròn và tia Oz vuông góc với AB. ( các tia Ax, By, Oz cùng phía với nửa đường tròn đối với AB). Gọi E là điểm bất kì của nửa đường tròn. Qua E vẽ tiếp tuyến với nửa đường tròn , cắt Ax, By, Oz theo thứ tự ở C,D,M. Chứng minh rằng khi điểm E thay đổi vị trí trên đường tròn thì điểm M chạy trên một tia.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

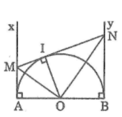
Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
O I 2 = MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra : AM.BN = O I 2 = R 2

bạn tự vẽ hình giúp mik nha
a) áp dụng t/c 2 tiếp tuyến cắt nhau ta có
OM là tia phân giác \(\widehat{AOI}\)
ON là tpg \(\widehat{IOB}\)
mà:\(\widehat{AOI}+\widehat{BOI}=180^o\)\(\Rightarrow OM\perp ON\)(t/c 2 góc kề bù)
vậy \(\widehat{MON}=90^o\)
b)từ t/c 2 tiếp tuyến cắt nhau ta có
MA=MI;BN=NI
\(\Rightarrow\)AM+BN=MI+NI=MN9(đpcm)
c)ta có:AM.BN=MI.NI(1)
xét \(\Delta MON\) vuông tại O có
MI.NI(đlý)=\(OI^2=R^2\)(2)
từ (1) và (2)\(\Rightarrow AM.BN=R^2\)

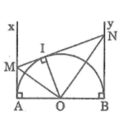
Gọi I là tiếp điểm của tiếp tuyến MN với đường tròn (O). Nối OI
Ta có: ![]() (hai góc kề bù)
(hai góc kề bù)
OM là tia phân giác của góc AOI (tính chất hai tiếp tuyến cắt nhau)
ON là tia phân giác của góc BOI (tính chất hai tiếp tuyến cắt nhau)
Suy ra : OM ⊥ ON (tính chất hai góc kề bù)
Vậy ![]()

b: Xét (O) có
MC là tiếp tuyến
MA là tiếp tuyến
Do đó: MC=MA
Xét (O) có
NC là tiếp tuyến
NB là tiếp tuyến
Do đó: NC=NB
Ta có: MN=MC+NC
nên MN=MA+NB

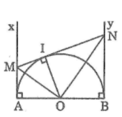
Ta có: MA = MI (tính chất hai tiếp tuyến cắt nhau)
NB = NI (tính chất hai tiếp tuyến cắt nhau)
Mà: MN = MI + IN
Suy ra: MN = AM + BN

a: Xét (O) có
MI,MA là tiếp tuyến
nên MI=MA và OM là phân giác của góc AOI(1)
Xét (O) có
NI,NB là tiếp tuyến
nên NI=NB và ON là phân giác của góc IOB(2)
Từ (1), (2) suy ra góc MON=1/2*180=90 độ
b: MN=MI+IN
=>MN=MA+NB
c: Gọi H là trung điểm của MN
Xét hình thang AMNB có
O,H lần lượt là trung điểm của AB,MN
nên HO là đường trung bình
=>HO//AM//BN
=>HO vuông góc AB
=>AB là tiếp tuyến của(H)

a: Xét (O) có
CE là tiếp tuyến có E là tiếp điểm
CA là tiếp tuyến có A là tiếp điểm
Do đó: CE=CA
Xét (O) có
DB là tiếp tuyến có B là tiếp điểm
DE là tiếp tuyến có E là tiếp điểm
Do đó: DB=DE
Ta có: CD=CE+ED
nên CD=CA+DB

a: Xét (O) có
CE là tiếp tuyến
CA là tiếp tuyến
Do đó: CE=CA
Xét (O) có
DE là tiếp tuyến
DB là tiếp tuyến
Do đó: DE=DB
Ta có: CE+DE=CD
nên CD=CA+DB
Câu này hơi kì, vì đề đã nói rõ tiếp tuyến cắt Oz tại M, thế thì M chạy trên tia Oz còn hỏi gì nữa???
mình nghĩ câu này, nên "giấu" cái Oz đi, mà cho M là trung điểm của CD, làm thế nhé
Thấy tứ giác ABDC là hình thang vuông, có OM là đường trung bình (qua trung điểm 2 cạnh bên)
=> OM // Ax // By => M chạy trên tia qua O và // Ax (chính là Oz)
mơn bạn nha