Cho ba số a, b, c thỏa mãn ba điều kiện sau: a < b < c; 11 < a < 15; 12 < c < 15. Khi đó a + b + c =
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Từ điều kiện 91≤a≤93 và a ∈ ¥ ta suy ra: a ∈ {91;92;93}
Từ điều kiện 91<c<94 và c ∈ ¥ ta suy ra: c ∈ {92;93}
Mặt khác, a<b<c (b là số tự nhiên) nên a = 91; b = 92; c = 93

Ta có:

Dấu “=” xảy ra khi và chỉ khi


Vậy số bộ a,b,c thỏa mãn điều kiện đã cho là 1.
Chọn B.


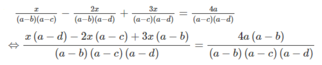
⇔ x(a − d) − 2x(a − c) + 3x(a − b) = 4a(a − b)
⇔ x(a − d − 2a + 2c + 3a − 3b) = 4a(a − b)
⇔ x(2a − 3b + 2c − d) = 4a(a − b)
Theo giả thiết, b + d = 2c nên 2a – 3b + 2c – d = 2a – 2b = 2 (a – b ).
Do đó phương trình đã cho tương đương với phương trình 2(a − b)x = 4a(a − b)
Để ý rằng a – b ≠ 0, ta thấy ngay phương trình cuối có nghiệm duy nhất x = 2a.
Vậy phương trình đã cho cũng có nghiệm duy nhất x = 2a.

11<a<15
<=> a\(\in\left\{12;13;14\right\}\)
12<c<15
<=>c\(\in\left\{13;14\right\}\)
Mà a<b<c
<=>
a=12;b=13;c=14
Khi đó a+b+c=12+13+14=39