a) Tìm giá trị của x + y biết x - y = 2 , xy = 99 và y < 0
b) Giá trị của x + y biết x - y = 4 , xy = 5 và x < 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Có : (x - y)2 = 42 = 16
<=> x2 - 2xy + y2 = 16
<=> x2 - 2.5 + y2 = 16
<=> x2 + y2 = 26
Lại có :
x2 + 2xy + y2 = (x + y)2 = 26 + 2.5
<=> (x + y)2 = 36
=> \(\orbr{\begin{cases}x+y=6\\x+y=-6\end{cases}}\)
Lập luận : Ta thấy x < 0
mà xy = 5 >0
=> y < 0
=> x + y = < 0
Vậy x + y = -6
x = 4 + y thay vào pt xy=5 ta có pt :
y(4+y)=5 \(\Leftrightarrow\)y2 +4y -5 = 0 \(\Rightarrow\) ý = 1 và y = -5 thấy y lần lượt vào 1 pt ta có x = 5 và x = -1
xét điều kiện ta loại nghiệm x = 5 nhận nghiệm x= -1 ( y = -5)
vậy giá trị của x + y = -6

\(x-y=4\Leftrightarrow x^2+y^2-2xy=16\)\(\Leftrightarrow x^2+y^2=26\)\(\Leftrightarrow x^2+y^2+2xy=36\)\(\Leftrightarrow x+y=6\)hoặc\(-6\)
Mà xy=5,x<0 -->y<0 -->x+y=-6

ta có : (x-y)2=16
x2-2xy+y2=16
x2+y2=5.2+16
x2+2xy+y2-2xy=26
(x+y)2-2.5=26
(x+y)2-10=26
(x+y)2=26+10=36
suy ra x+y=6
x+y= -6
ta có nếu: x-y=4=>y=x -4
=>x+y= -6
<=>x+x -4= -6
2x= -2=>x= -1
nếu x+y=6
<=>x+x -4=6
2x=10
=> x=5
mà x<0 => x+y=-6

Sử dụng Bdt thức \(ab\le\left(\frac{a+b}{2}\right)^2\) với \(a,b>0\).
Tự chứng minh
\(------------------\)
Áp dụng bđt trên, ta có:
\(A=x^2y=\frac{1}{2}.2x.xy\le\frac{1}{2}\left(\frac{2x+xy}{2}\right)^2=\frac{1}{8}\left(2x+xy\right)^2=\frac{1}{8}.4^2=2\)
Dấu \("="\) xảy ra khi và chỉ khi \(\hept{\begin{cases}2x=xy\\2x+xy=4\end{cases}\Leftrightarrow\hept{\begin{cases}x=1\\y=2\end{cases}}}\)
Kết luận: .....


Câu 3:
a: A(x)=x^3+3x^2-4x-12
B(x)=x^3-3x^2+4x+18
A(x)+B(x)
=x^3+3x^2-4x-12+x^3-3x^2+4x+18
=2x^3+6
A(x)-B(x)
=x^3+3x^2-4x-12-x^3+3x^2-4x-18
=6x^2-8x-30
b: A(-2)=(-8)+3*4-4*(-2)-12
=-20+3*4+4*2=0
=>x=-2 là nghiệm của A(x)
B(-2)=(-8)-3*(-2)^2+4*(-2)+18=-10
=>x=-2 ko là nghiệm của B(x)

HD:
Dễ thấy b = 1, d = 2, e = 4 đặt y = x2 – 2 suy ra y2 = x4 – 4x2 + 4
Biến đổi P(x) = x4 – 4x2 + 4 – x3 – 6x2 + 2x
= (x2 – 2)2 – x(x2 – 2) – 6x2
Từ đó Q(y) = y2 – xy – 6x2
Tìm m, n sao cho m.n = - 6x2 và m + n = - x chọn m = 2x, n = -3x
Ta có: Q(y) = y2 + 2xy – 3xy – 6x2
= y(y + 2x) – 3x(y + 2x)
= (y + 2x)(y – 3x)
Do đó: P(x) = (x2 + 2x – 2)(x2 – 3x – 2).
a/ tìm GT của x+y biết x-y=2; x.y=99 và y<0^2=4)
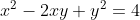
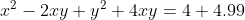
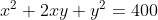
^2=400)
Vì x-y=2 nên
\(\Leftrightarrow\)
\(\Leftrightarrow\)
\(\Leftrightarrow\)
\(\Leftrightarrow\)
\(\Leftrightarrow\) x+y=20 hoặc x+y=-20
mà y<0 nên x+y=20