Cho một đường thẳng d chia tam giác ABC nhọn cho trước thành hai có diện tích bằng nhau và chu vi bằng nhau, Chứng minh tâm đường tròn nội tiếp tam giác ABC nằm trên đường thẳng d.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 5 2022
a: Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=180^0\)
nên AEHF là tứ giác nội tiếp
b: Xét tứ giác BFEC có \(\widehat{BFC}=\widehat{BEC}=90^0\)
nên BFEC là tứ giác nội tiếp
=>\(\widehat{FEC}+\widehat{ABC}=180^0\)
2 tháng 7 2023
a: góc BIH+góc BKH=180 độ
=>BIHK nội tiếp
b: OE vuông góc BC
=>sđ cung EB=sđ cung EC
=>góc BAE=góc CAE
Xét ΔAKB vuông tại K và ΔACF vuông tại C có
góc ABK=góc AFC
=>ΔAKB đồng dạng với ΔACF
=>góc BAK=góc CAF
=>góc DAE=góc FAE
=>AE là phân giác của góc DAF
CM
8 tháng 3 2019
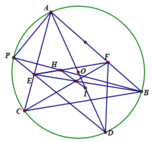
1). Gọi DE cắt (O) tại P khác D. Do AD là đường kính của (O), suy ra A P D ^ = 90 0 , mà A H E ^ = 90 0 ( do H E ∥ B C ⊥ H A ), nên tứ giác APEH nội tiếp.
Ta có A P H ^ = A E H ^ (góc nội tiếp)
= A C B ^ H E ∥ B C = A P B ^ (góc nội tiếp)
⇒ P H ≡ P B
2). Ta có H P ⊥ A C ⇒ A E H ^ = A H P ^ = A E P ^
Suy ra EA là phân giác ngoài đỉnh E của tam giác DEF
Tương tự FA là phân giác ngoài đỉnh F của tam giác DEF
Suy ra A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Do I là tâm nội tiếp nên EI là tia phân giác trong.
Mà EA là tia phân giác ngoài, suy ra E I ⊥ A C ⇒ E I ∥ H B
Tương tự F I ∥ H C ; E F ∥ B C ⇒ Δ I E F v à Δ H B C có cạnh tương ứng song song, nên BE; CF và IH đồng quy.
7 tháng 3 2016
Có vẻ bài này hơi không phù hợp với học sinh lớp 9. Đầu tiên ta sẽ phải sử dụng định lý sin cho tam giác: Trong tam giác ABC với bán kính đường tròn ngoại tiếp R thì tỷ số giữa cạnh và sin góc đối diện bằng 2R. Nhận xét tiếp theo: Diện tích tam giác bất kỳ một nửa tích độ dài hai cạnh nhân với sin của góc xen giữa hai cạnh đó.
Ta có \(S\left(ABC\right)=S\left(ABF\right)+S\left(ACF\right)=\frac{1}{2}AB\cdot AF\cdot\sin BAF+\frac{1}{2}AC\cdot AF\cdot\sin CAF\)
\(=\frac{1}{2}AB\cdot\frac{CD}{2R}\cdot AF+\frac{1}{2}AC\cdot AF\cdot\frac{BD}{2R}=\frac{AF}{4R}\left(AB\cdot CD+AC\cdot BD\right).\) Do tứ giác ABDC nội tiếp nên theo định lý Ptoleme ta có \(AB\cdot CD+AC\cdot BD=AD\cdot BC.\) LSuy ra \(S\left(ABC\right)=\frac{AF\cdot AD\cdot BC}{4R}.\)
Tiếp theo ta có \(S\left(AMDN\right)=S\left(AMD\right)+S\left(ADN\right)=\frac{1}{2}AM\cdot AD\cdot\sin BAD+\frac{1}{2}AD\cdot AN\cdot\sin DAC\)
\(=\frac{1}{2}AF\cdot\cos DAC\cdot AD\cdot\sin BAD+\frac{1}{2}AD\cdot AF\cdot\cos BAD\cdot\sin DAC\)
\(=\frac{1}{2}AF\cdot AD\cdot\left(\cos DAC\cdot\sin BAD+\sin DAC\cdot\cos BAD\right)=\frac{1}{2}\cdot AF\cdot AD\sin\left(DAC+BAD\right)\)
\(=\frac{1}{2}AF\cdot AD\cdot\sin BAC=\frac{1}{2}AF\cdot AD\cdot\frac{BC}{2R}=\frac{AF\cdot AD\cdot BC}{4R}.\)
Ở đây ta sử dụng công thức hình chiếu \(\sin\left(a+b\right)=\sin a\cos b+\cos a\sin b.\)
Vậy ta có tứ giác AMDN và tam giác ABC cùng diện tích.
8 tháng 4 2020
Karin Korano
câu hỏi này của lớp 11 nhé !
1 cách trình bày khác; ngắn gọn hơn nha Thầy Giáo Toán
đặt ^BAE=^CAE=α; EAF=β
Ta có S∆ABC =1/2.AB.AF.sin(α+β)+1/2 .AC.AF sin α =AF/4R (AB.CD+AC.BD)
(R-là bán kính đường tròn ngoại tiếp tam giác ABC) (1)
Diện tích tứ giác ADMN là
SADMN =1/2.AM.AD.sin α +1/2AD.AN.sin(α+β) = 1/2.AD.AF.sin(2α +β) =AF/4R.AD.BC (2)
Vì tứ giác ABDC nội tiếp trong đường tròn nên theo định lí Ptoleme ta có
: AB.CD + AC.BD = AD.BC (3).
Từ (1), (2), (3) ta có điều phải chứng minh
GN
27 tháng 5 2018
B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)
