Cho hình thang ABCD (AB//CD), M là trung điểm của AD ,N là trung điểm của BC .Gọi IK theo thứ tự là giao điểm của MN với BC, AC. Cho biết AB=6cm ,CD=14cm Tính các độ dài MI,IK,KN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
14 tháng 7 2017
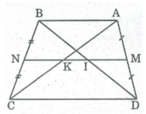
Hình thang ABCD có AB // CD
M là trung điểm của AD (gt)
N là trung điểm của BC (gt)
Nên MN là đường trung bình của hình thang ABCD ⇒ MN//AB// CD
MN = (AB + CD) / 2 = (6 + 14) / 2 = 10 (cm)
* Trong tam giác ADC, ta có:
M là trung điểm của AD
MK // CD
⇒ AK= KC và MK là đường trung bình của ∆ ADC.
⇒ MK = 1/2 CD = 1/2 .14= 7 (cm)
Vậy: KN = MN – MK = 10 – 7 = 3 (cm)
* Trong ∆ ADB, ta có:
M là trung điểm của AD
MI // AB nên DI = IB
⇒ MI là đường trung bình của ∆ DAB
⇒ MI = 1/2 AB = 1/2 .6 = 3 (cm)
IK = MK – Ml = 7 – 3 = 4 (cm)
22 tháng 8 2016
+) Hình thang ABCD có M;N là trung điểm của AD; BC => MN là đường trung bình của hình thang
=> MN // AB//CD và MN = (AB + CD) /2 = 10 cm
+) Xét tam giác ABD có: M là trung điểm của AD; MI // AB
=> I là trung điểm của DB
=> MI là đường trung bình của tam giác ABD => MI = AB?2 = 6/2 = 3cm
+) Xét tam giác CAB có: N là trung điểm của BC; NK //AB => K là trung điểm của AC
=> NK là đường trung bình của tam giác ABC
=> NK = AB / 2 = 6/2 = 3 cm
+) MN = MI + IK + KN = 3 + IK + 3 = 6 + IK = 10 => IK = 4 cm
xét hthang ABCD có: M là t/đ của AD(gt) , N là t/đ của BC(gt)
=> MN là đg trung bình của hthang ABCD=> MN//AB//CD và MN = 1/2 . (AB+CD) (1)
xét tg ABD có: M là t/đ của AD(gt) , MI//AB (vì I thuộc MN , MN//AB) => I là t/đ của BD=> MI là đg trung bình của tg ABD
=> MI=1/2.AB => MI= 1/2.6=3(cm) (vì AB=6 cm)
c/m tương tự ta đc: KN là đg trung bình của tg ABC => KN = 1/2. AB = 1/2.6 =3 (cm) (vì AB =6cm)
Mặt khác : MN= MI +IK +KN => MN=3 +IK +3 => MN= 6+ IK (2)
Từ (1),(2) => 6+ IK = 1/2. (AB+CD)
<=> 6+IK =1/2.(6+14)
<=> 6+ IK= 10
<=> IK =4 (cm)