Cho tứ giác lồi ABCD , 2 đường chéo AC và BD vuông góc với nhau biết AC=m , BD=n , gọi EF là trung điểm của AB và CD . Tính EF
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


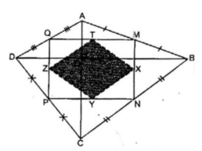
Kẻ đường chéo MP và NQ
Trong △ MNP ta có:
X là trung điểm của MN
Y là trung điểm của NP
nên XY là đường trung bình của △ MNP
⇒ XY // MP và XY = 1/2 MP (tính chất đường trung bình của tam giác) (3)
Trong △ QMP ta có:
T là trung điểm của QM
Z là trung điểm của QP
nên TZ là đường trung bình của △ QMP
⇒ TZ // MP và TZ = 1/2 MP (tính chất đường trung bình của tam giác) (4)
Từ (3) và (4) suy ra: XY // TZ và XY = TZ nên tứ giác XYZT là hình bình hành.
Trong △ MNQ ta có XT là đường trung bình
⇒ XT = 1/2 QN (tính chất đường trung bình của tam giác)
Tứ giác MNPQ là hình chữ nhật ⇒ MP = NQ
Suy ra: XT = XY. Vậy tứ giác XYZT là hình thoi
S X Y Z T = 1/2 XZ. TY
mà XZ = MQ = 1/2 BD = 1/2. 8 = 4 (cm);
TY = MN = 1/2 AC = 1/2 .6 =3 (cm)
Vậy : S X Y Z T = 1/2. 3. 4 = 6( c m 2 )

Xét $(O)$ có: $\widehat{ACD}=\widehat{ABD}=90^o$( góc nội tiếp chắn nửa đường tròn)
suy ra $\widehat{ECD}=90^o$
$\widehat{BAC}=\widehat{BDC}$ (các góc nội tiếp cùng chắn cung $BC$)
hay $\widehat{BAE}=\widehat{EDC}(1)$
Xét tứ giác $BEFA$ có: $\widehat{ABE}=\widehat{EFA}=90^o$ (do $EF AD$)
nên $\widehat{ABE}+\widehat{EFA}=180^o$
suy ra tứ giác $BEFA$ nội tiếp
suy ra $\widehat{EFB}=\widehat{BAE}(2)$ (các góc nội tiếp cùng nhắn $BE$)
Chứng minh tương tự ta có: tứ giác $ECDF$ nội tiếp nên $\widehat{EFC}=\widehat{EDC}(3)$ (các góc nội tiếp cùng chắn cung $EC$)
Từ $(1)(2)(3)$ suy ra $\widehat{EFB}+\widehat{EFC}=\widehat{BAE}+\widehat{EDC}=2.\widehat{EDC}$
hay $\widehat{BFC}=2.\widehat{EDC}$
Lại có: tam giác $ECD$ vuông tại $C$
$M$ là trung điểm $ED$
Nên $EM=MD=CM$
Suy ra tam giác $MCD$ cân tại $M$
nên $\widehat{MCD}=\widehat{MDC}$
Lại có: $\widehat{BMC}$ là góc ngoài tam giác $MCD$ nên
$\widehat{BMC}=\widehat{MCD}+\widehat{MDC}=2.\widehat{MDC}=2.\widehat{EDC}
Mà $\widehat{BFC}=2.\widehat{EDC}$
nên $\widehat{BMC}=\widehat{BFC}$
suy ra $F;M$ cùng nhìn đoạn $BC$ dưới 1 góc ko đổi
$F;M$ là 2 đỉnh liên tiếp tứ giác $BCMF$
suy ra tứ giác $BCMF$ nội tiếp (Bài toan quỹ tích cung chứa góc)