so sánh phân số ;
a)\(\frac{29}{33};\frac{22}{37};\frac{29}{37}\)b)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 4 2019
*Nhớ lại: Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
Mẫu: So sánh: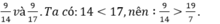 
b) So sánh: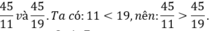
CM
8 tháng 11 2018
*Nhớ lại: Trong hai phân số có cùng tử số, phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.
Mẫu: So sánh: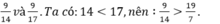 
a) So sánh: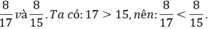
21 tháng 2 2022
a) ta có: \(1-\frac{2012}{2013}=\frac{1}{2013}\)
\(1-\frac{2013}{2014}=\frac{1}{2014}\)
mà \(\frac{1}{2013}>\frac{1}{2014}\) nên \(\frac{2013}{2014}>\frac{2012}{2013}\)
3 tháng 6 2015
Ta có:
\(\frac{2}{5}=\frac{8}{20};\frac{4}{2}=\frac{40}{20};\frac{6}{2}=\frac{60}{20};\frac{9}{4}=\frac{45}{20};\frac{5}{4}=\frac{25}{20}\)
Vì \(\frac{8}{20}
CM
15 tháng 10 2018
Khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai hoặc khi tử số của phân số thứ nhất lớn hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại nhỏ hơn mẫu số của phân số thứ hai thì ta có thể so sánh hai phân số bằng phương pháp so sánh với phân số trung gian.
Do đó cả hai đáp án A và B đều đúng
Đáp án cần chọn là D
CM
29 tháng 12 2018
Khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai hoặc khi tử số của phân số thứ nhất lớn hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại nhỏ hơn mẫu số của phân số thứ hai thì ta có thể so sánh hai phân số bằng phương pháp so sánh với phân số trung gian.
Do đó cả hai đáp án A và B đều đúng.
Đáp án D.
6 tháng 3 2021
Ta có : 17/40 < 17/37 <18/37
Suy ra 17/40 < 18/37
\(\frac{22}{37}\) < \(\frac{29}{37}\) < \(\frac{29}{33}\)
Ghi nhớ : Muốn so sánh phân số , ta lấy tử chia cho mẫu
\(\frac{22}{37}\)< \(\frac{29}{37}\)<\(\frac{29}{33}\)