Thay 1 chữ số bằng một số thích hợp,những chữ giống nhau được thay bằng những chữ số giống nhau để được phép tính:
a00b+b00a=7cc2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 5 2020
Toán lớp 3 thì chắc làm theo thế này!
c + c + c = 9 hoặc 19 ( loại )
=> c = 3
b + b = 8 hoặc 18
=> b = 4 hoặc b = 9
=> a = 7 hoặc a = 6
Thử lại với a = 7; b = 4 ; c = 3 ta có:
743 + 43 + 3 = 789 ( thỏa mãn )
Thử lại với a = 6; b = 9; c = 3, ta có:
693 + 93 + 3 = 789 ( thỏa mãn )
Vậy a = 7; b = 4; c = 3 hoặc a = 6; b = 9; c = 3.
4 tháng 5 2020
Khi ta dặt tính theo cột dọc. ta thấy: c + c + c = 9
Vậy c = 3
b + b = 8
Vậy b = 4
a = 7
Đ/S: a = 7
b = 4
c = 3
CM
19 tháng 5 2017
- Vì A≠G mà chữ số hàng chục của tổng là 0 nên phép cộng có nhớ 1 sang hàng trăm nên ở hàng trăm: H + N + 1 (nhớ) = 10; nhớ 1 sang hàng nghìn. Do đó H + N = 10 - 1 = 9.
- Phép cộng ở hàng nghìn: N + 1 (nhớ) = 2 nên N = 2 - 1 = 1.
Thay N = 1 ta có: H + 1 = 9 nên H = 9 - 1 = 8
- Phép cộng ở hàng đơn vị: Có 2 trường hợp xảy ra:
* Trường hợp 1: Phép cộng ở hàng đơn vị không nhớ sang hàng chục.
Khi đó: M + O = 0 và A + G = 10.
Ta có bảng: (Lưu ý 4 chữ M, O, A, G phải khác nhau và khác 1; 8)
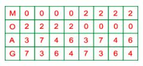
* Trường hợp 2: Phép cộng ở hàng đơn vị có nhớ 1 sang hàng chục.
Khi đó: M + O = 12 và A + G = 9. Ta có bảng:
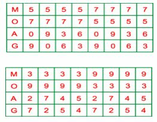
Vậy bài toán có 24 đáp số như trên.
5 tháng 11 2017
ong số học, bội số chung nhỏ nhất (hay còn gọi tắt là bội chung nhỏ nhất, viết tắt là BCNN, tiếng Anh: least common multiple hoặc lowest common multiple (LCM) hoặc smallest common multiple) của hai số nguyên a và b là số nguyên dương nhỏ nhất chia hết cho cả a và b.[1] Tức là nó có thể chia cho a và b mà không để lại số dư. Nếu a hoặc b là 0, thì không tồn tại số nguyên dương chia hết cho a và b, khi đó quy ước rằng LCM(a, b) là 0.
Định nghĩa trên đôi khi được tổng quát hoá cho hơn hai số nguyên dương: Bội chung nhỏ nhất của a1,..., an là số nguyên dương nhỏ nhất là bội số của a1,..., an.
