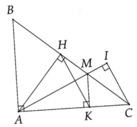
Cho tam giác ABC cân tại A. Đường cao AH. Gọi I là hình chiếu của H trên AC. Gọi M là trung điểm của HI. Chứng minh BI vuông góc với AM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 8 2017
*Bạn tự vẽ kình nha
a) Xét \(\Delta\) IHC có J, M là trung điểm của IH,IC
=> JM là đường trung bình
=> +) JM = 1/2 HC
+) JM // HC
Có AK // BC mà H thuộc BC => AK // HC
mà JM // HC (cmt)
=>AK // JM
Lại có N là trung điểm của AK => +) N\(\in\)AK
mà AK // JM (cmt) => AN // JM (1)
+) AN = 1/2 AK
Xét tứ giác AKNH có AK // Hc , AH // KC
=> AKNH là hình bình hành => AK = HC
Có : AN = 1/2 AK
JM = 1/2 HC
=> AN = JM (2)
Từ (1) và (2) => tứ giác ANMJ là hình bình hành
10 tháng 8 2017
Xem lại đề nhà bạn, BI vuông góc với MN thì hơi vô lí, BI vuông góc với AN thôi
24 tháng 10 2018
Gọi O là giao điểm của AH và IK, N là giao điểm của AM và IK. Ta có
MAK = MCK, OKA = OAK nên
MAK + OKA = MCK + OAK = 90 độ
Do đó AM vuông góc IK
11 tháng 8 2017
1) Ta có:
\(\hept{\begin{cases}IM=\frac{1}{2}HC\\AN=\frac{1}{2}AK\\HC=AK\end{cases}}\)\(\Rightarrow IM=AN\)
mà IM // AN
\(\Rightarrow\)AJMN là hình bình hành.
