Cho hình chữ nhật ABCD ,có AB = 8 ,BC = 6 vẽ đường cao AH của tam giác ADB .a)tính BD.b)Chứng minh rằng tam giác ADH đồng dạng với tam giác ADBc)CM.ADbinh phương=DH.DB.d)Chứng minh rằng tam giác AHB đồng dạng với tam giác BCD.e) Tính độ dài DH,AH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)
Do đó: ΔAHB\(\sim\)ΔBCD
b: Xét ΔADH vuông tại H và ΔBDA vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔADH\(\sim\)ΔBDA
Suy ra: \(\dfrac{AD}{BD}=\dfrac{HD}{DA}\)
hay \(AD^2=HD\cdot BD\)
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
Do đó: ΔAHBΔBCD
b: Xét ΔADH vuông tại H và ΔBDA vuông tại A có
chung
Do đó: ΔADHΔBDA
Suy ra:
hay

Hình:
~~~~~
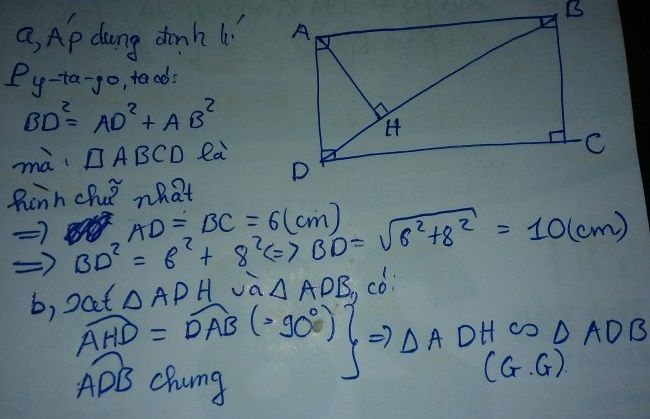
a/ Vì ABCD là hcn nên: AD = BC = 6cm
A/dung đli Pytago vào tam giác ABD vuông tại A có:
\(BD^2=AB^2+AD^2=8^2+6^2=100\)
\(\Rightarrow BD=10cm\)
b/ Xét ΔADH và ΔADB có:
\(\widehat{H_1}=\widehat{BAD}=90^o\left(gt\right)\)
\(\widehat{D_1}:chung\)
=> ΔHDA ~ ΔADB (g.g) (đpcm)
c/ Vì ΔHDA ~ ΔADB nên:
\(\dfrac{DH}{AD}=\dfrac{AD}{DB}\Rightarrow AD^2=DH\cdot DB\left(đpcm\right)\)
d/ Xét ΔAHB và ΔBCD có:
\(\widehat{H_2}=\widehat{C}=90^o\) (gt)
\(\widehat{B_2}=\widehat{D_2}\left(so.le.trong\right)\)
=> ΔAHB ~ ΔBCD (g.g) (đpcm)
e/ Có: AD2 = DH . DB
=> DH = \(\dfrac{AD^2}{DB}=\dfrac{6^2}{10}=3,6\) (cm)
+) AH = \(\sqrt{AD^2-DH^2}=\sqrt{6^2-3,6^2}=\) 4,8 (cm) (A/dung định lí pytago)

a) Xét tam giác AHD và tam giác BHA có:
ADH = BAH ( cùng phụ với DAH )
DAH = ABH ( cùng phụ với BAH )
=> tam giác AHD đồng dạng với BHA (g.g)
b) Xét tam giác ABH và tam giác DBA có:
Chung góc B; BHA = BAD(=90 độ)
=> tam giấc ABH đồng dạng tam giác DBA (g.g)
c)

a: Xét ΔABD vuông tại A có
\(BD^2=AB^2+AD^2\)
nên BD=10(cm)
b: Xét ΔADH vuông tại H và ΔBDA vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔADH\(\sim\)ΔBDA


help me....huhu