1 xe cần chở 120 tấn hàng. Hôm làm việc có 2 xe phải điều đi nơi khác nên mỗi chiếc xe còn lại phải chở thên 16 tấn .Hỏi đội xe có bao nhiêu xe
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 12 2019
Gọi số xe ban đầu là x, (x ∈ ℕ * , x > 5, xe)
* Theo dự định: Tổng số hàng là: 150 (tấn)
Số hàng mỗi xe chở là: 150/x (tấn)
* Thực tế: Tổng số xe là x – 5 (xe)
Số hàng mỗi xe chở là: 150/(x-5) (tấn)
Vì số hàng thực tế mỗi xe chở hơn dự định 5 tấn nên ta có phương trình:
Vậy số xe ban đầu của đội là 15 xe
Đáp án: C
2 tháng 3 2020
Gọi x là số xe của đội là a
Nếu toàn bộ xe mỗi xe phải chở \(\frac{120}{a}\)(tấn hàng)
Mà khi chuyên chở phải chở:\(\frac{120}{\left(a-2\right)}\) (tấn hàng)
Theo đề bài ta có
Khi chuyển chở đi nơi khác mỗi xe phải chở 16 tấn hàng nên ta lập PT sau:
\(\frac{120}{a}+16=\frac{120}{\left(a-2\right)}\)
giải PT sau ta được a=5 (xe)
C
16 tháng 5 2022
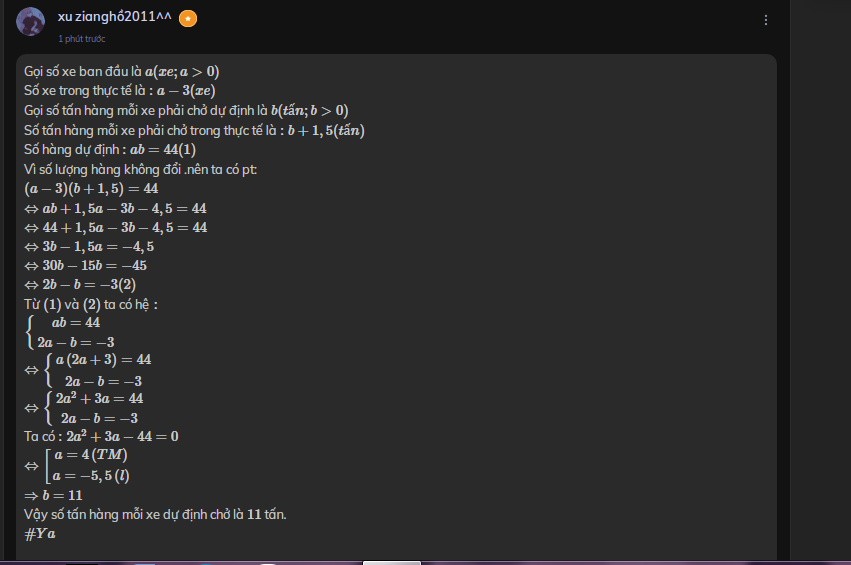
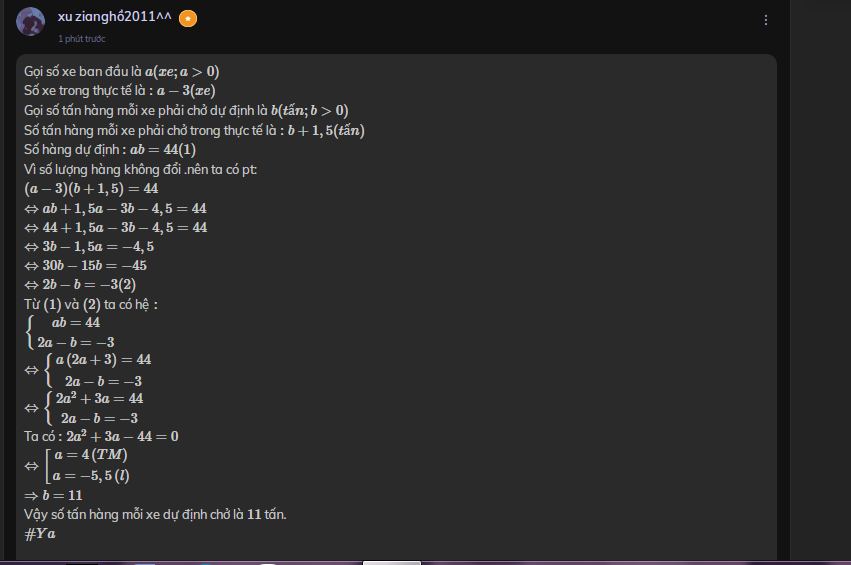
Gọi số xe ban đầu là \( a ( xe ; a > 0 )\)
Số xe trong thực tế là \(: a − 3 ( xe ) \)
Gọi số tấn hàng mỗi xe phải chở dự định là \(b( tấn ; b > 0 )\)
Số tấn hàng mỗi xe phải chở trong thực tế là \(:b + 1 , 5 ( tấn ) \)
Số hàng dự định \(:a b = 44 ( 1 )\)
Vì số lượng hàng không đổi .nên ta có pt:
\(( a − 3 ) ( b + 1 , 5 ) = 44\)
\(⇔ a b + 1 , 5 a − 3 b − 4 , 5 = 44\)
\(⇔ 44 + 1 , 5 a − 3 b − 4 , 5 = 44\)
\(⇔ 3 b − 1 , 5 a = − 4 , 5\)
\(⇔ 30 b − 15 b = − 45\)
\(⇔ 2 b − b = − 3 ( 2 )\)
Từ `(1)` và `(2)` ta có hệ `:`
\(\left\{{}\begin{matrix}ab=44\\2a-b=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a\left(2a+3\right)=44\\2a-b=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a^2+3a=44\\2a-b=-3\end{matrix}\right.\)
Ta có \(:2a^2+ 3 a − 44 = 0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=4\left(TM\right)\\a=-5,5\left(l\right)\end{matrix}\right.\)
\(⇒ b = 11\)
Vậy số tấn hàng mỗi xe dự định chở là `11` tấn.
`#Ya`
14 tháng 6 2023
Gọi số xe ban đầu là x
Theo đề, ta có: 44/(x-3)-44/x=1,5
=>\(\dfrac{44x-44x+132}{x\left(x-3\right)}=\dfrac{3}{2}\)
=>3x^2-9x=264
=>x=11
30 tháng 5 2021
gọi số xe lúc đầu : x(xe)(x>2)
số xe lúc sau khi có 2 xe bị điều đi :x-2(xe)
theo dự định mỗi xe chở :\(\dfrac{120}{x}\)(tấn hàng)
thực tế mỗi xe chở :\(\dfrac{120}{x-2}\)(tấn hàng)
vì thực tế mỗi xe phải chở thêm 3 tấn
=>\(\dfrac{120}{x}=\dfrac{120}{x-2}-3\)
giải pt trên ta tìm đc :\(\left\{{}\begin{matrix}x1=10\left(TM\right)\\x2=-8\left(loai\right)\end{matrix}\right.\)vậy ban đầu có 10 xe
