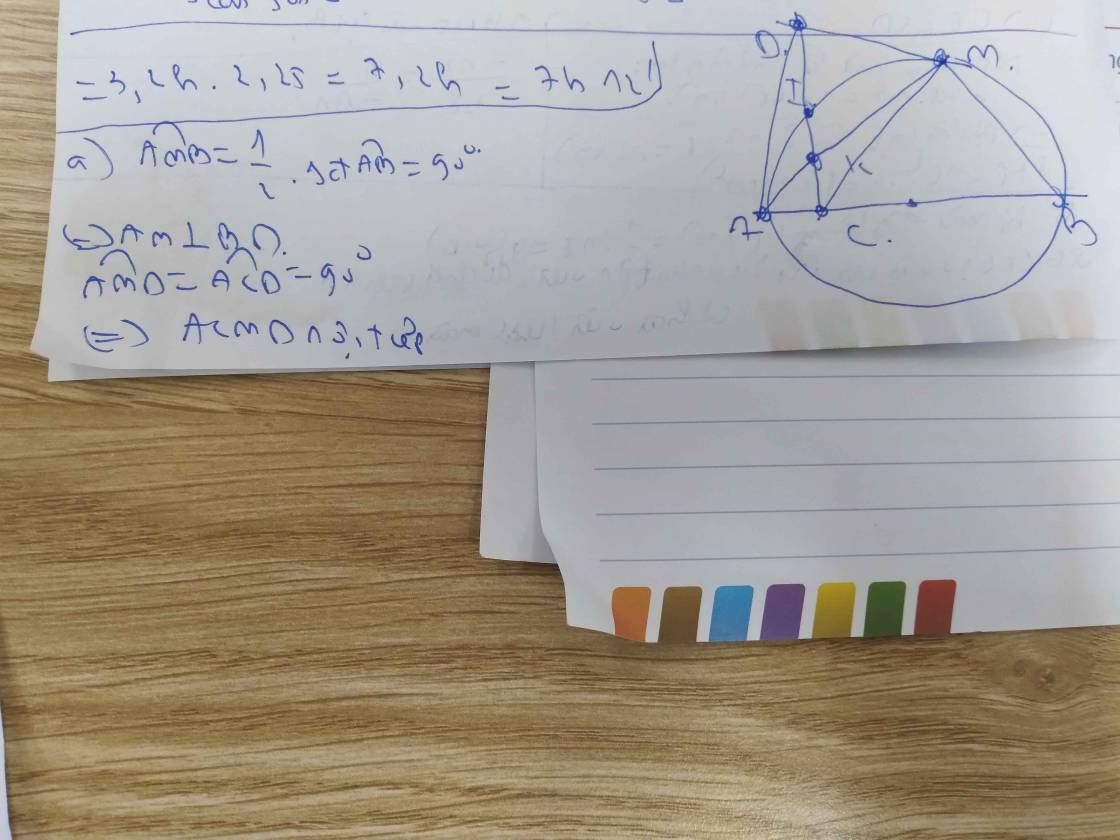
Cho nửa đường tròn tâm (O) có đường kính AB.lấy điểm C trên đoạn thẳng AO (C khác A, C khác O). Đường thẳng đi qua C và vuông góc với AB cắt nửa đường tròn tại K. Gọi M là điểm bất kì trên cung AB ( M khác K, M khác B). Đường thẳng CK cắt các đường thẳng AM,BM lần lượt tại H và D. Đường thẳng BH cắt nửa đường tròn tại điểm thứ hai N
a) chứng minh: ACMD nội tiếp
b) chứng minh: CA.CB= CH.CD
c) Chứng minh; ba điểm A,N,D thẳng hàng và tiếp tuyến tại N của nửa đường tròn đi qua trung điểm của DN
d) khi M di chuyển trên cung KB. chứng minh đường thẳng MN luôn đi qua 1 điểm cố định.