Chứng minh rằng không thể thay các chữ bằng các số để nó phép tính đúng:
a, HỌC VUI - VUI HỌC = 1991
B, TOÁN + LÍ + SỬ + VẼ = 1992
( giải ra dùm, camon )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải
a) Hai số HỌC VUI, VUI HỌC có tổng các chữ số như nhau nên có cùng số dư khi chia cho 9, do đó hiệu của chúng chia hết cho 9. Vế trái của ( 1 ) chia hết cho 9, còn vế phải không chia hết cho 9. Vậy không thể có phép tính đúng.
b) Chú ý rằng, một số và tổng của các chữ số của nó có cùng số dư khi chia cho 9. Do đó số dư của vế trái của ( 2 ) khi chia cho 9 bằng số dư của tổng T + O + Á + N + L + Í + S + Ử + V + Ẽ khi chia cho 9. Ta lại chú ý rằng 10 chữ số trên khác nhau nên tổng của chúng bằng :
0 + 1 + 2 + ...... + 9 = 45. Tổng này chia hết cho 9, suy ra vế trái của ( 2 ) chia hết cho 9, còn vế phải không chia hết cho 9. Vậy không thể có phép tính đúng.

bạn bảo là chứng minh mà, sao ko chứng minh vậy
Ai chả bt là k thể thay !!!!!!!
Không thể thay thế các chữ bằng các chữ số để có phép tính đúng là
HOC VUI - VUI HOC = 2004

Toán ,lí , sữ,vẽ đều là các môn học suy ra chúng bằng nhau
2017 không chia hết cho 4(môn) suy ra không thể thay các chữ số này

Mình giải được nè :
Ta có : HOCVUI , VUIHOC đều là số có 6 chữ số mà 2004 lại là số có 4 chữ số => ko thể thay được
Vũ Hoàng ơi nhớ k 5 cái cho tớ đó nha

- Vì A≠G mà chữ số hàng chục của tổng là 0 nên phép cộng có nhớ 1 sang hàng trăm nên ở hàng trăm: H + N + 1 (nhớ) = 10; nhớ 1 sang hàng nghìn. Do đó H + N = 10 - 1 = 9.
- Phép cộng ở hàng nghìn: N + 1 (nhớ) = 2 nên N = 2 - 1 = 1.
Thay N = 1 ta có: H + 1 = 9 nên H = 9 - 1 = 8
- Phép cộng ở hàng đơn vị: Có 2 trường hợp xảy ra:
* Trường hợp 1: Phép cộng ở hàng đơn vị không nhớ sang hàng chục.
Khi đó: M + O = 0 và A + G = 10.
Ta có bảng: (Lưu ý 4 chữ M, O, A, G phải khác nhau và khác 1; 8)
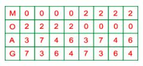
* Trường hợp 2: Phép cộng ở hàng đơn vị có nhớ 1 sang hàng chục.
Khi đó: M + O = 12 và A + G = 9. Ta có bảng:
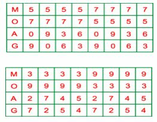
Vậy bài toán có 24 đáp số như trên.
a) Hai số HỌC VUI, VUI HỌC có tổng các chữ số như nhau nên có cùng số dư khi chia cho 9, do đó hiệu của chúng chia hết cho 9. Vế trái của ( 1 ) chia hết cho 9, còn vế phải không chia hết cho 9. Vậy không thể có phép tính đúng.
b) Chú ý rằng, một số và tổng của các chữ số của nó có cùng số dư khi chia cho 9. Do đó số dư của vế trái của ( 2 ) khi chia cho 9 bằng số dư của tổng T + O + Á + N + L + Í + S + Ử + V + Ẽ khi chia cho 9. Ta lại chú ý rằng 10 chữ số trên khác nhau nên tổng của chúng bằng :
0 + 1 + 2 + ...... + 9 = 45. Tổng này chia hết cho 9, suy ra vế trái của ( 2 ) chia hết cho 9, còn vế phải không chia hết cho 9. Vậy không thể có phép tính đúng.
Mình sẽ tính ra nhưng dấu có tính không vậy?