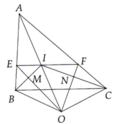
Cho tam giác ABC cân tại A. Phân giác BN và CM cắt nhau tại O. Gọi I là trung điểm của BC, K là trung điểm của MN. Từ O kẻ đường thẳng song song với BC, cắt AB và AC lần lượt tại P,Q.
a) C/m: tứ giác BMNC là hình thang cân.
b) C/m: BM=MN=NC
c) C/m: OM=ON
d) C/m: OP=OQ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
9 tháng 9 2020
c/
Xét tg BMC và tg CNB có
BC chung
tg ABC cân nên ^B=^C
=> ^MCB=^NBC=^C/2=^B/2
=> tg BMC = tg CNB (g.c.g) => BM=CN và ^BMC=^CNB
Xét tg OBM và tg OCN có
BM=CN và ^BMC = ^CNB (cmt)
^MBN = ^MCN = ^B/2=^C/2
=> tg OBM = tg OCN (g.c.g) => OM=ON và OB=OC
d/
Xét tg BOP và tg COQ có
OB=OC (c/m ở câu c)
^POB = ^OBC (góc sole trong)=^B/2; ^QOC = ^OCB = ^C/2 (góc so le trong) => ^POB = ^QOC
^PBO = ^QCO = ^B/2 = ^C/2
=> tg BOP = tg COQ (g.c.g) => OP = OQ
e/ Nối A với O cắt MN tại K' và BC tại I'
Xét tg ABC có O là giao 3 đường phân giác => AO là phân giác của ^A
mà ABC cân tại A => AO cũng là đường trung tuyến => I' là trung điểm của BC nên I trùng I'
Ta có
BM=CN (c/m ở câu c) mà AB=AC => AM=AB-BM=AN=AC-CN => tg AMN cân tại A
=> AO cũng là đường trung tuyến của tg AMN => K' là trung điểm của MN => K trùng K'
=> A, I, O, K đều nằm trên đường phân giác của ^A nên 4 điểm trên thẳng hàng
5 tháng 3 2022
Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành
