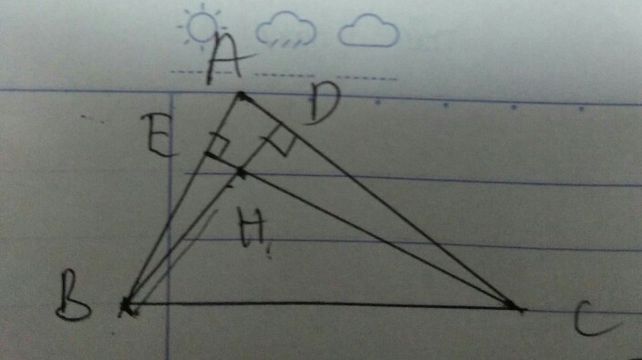
Tam giác nhọn ABC, có AB<AC. Các đường cao BE và CF cắt nhau tại O. Trên tia đối của tia BE lấy điểm G sao cho BG=AC; trến tia đối của tia CF lấy điểm H sao cho CH=AB. Trên tia đối của tia tia CF lấy điểm H sao cho CH=AB
a) CMR: \(\Delta AGB=\Delta HAC\)
b) CM \(AG⊥AH\)
c) Gọi M là trung điểm của GH, N là giao điểm của BC và GH
- Cm: \(\widehat{OAM}=\widehat{BNG}\)
- So sánh số đo 2 góc ^BAM=^MAC
Mk làm ok câu a và b rùi. Giúp mk câu c nha. Thanks nhìu !!!!!!!!!! ^^

Ta có AB < AC, mà AC = BG nên AB < BG. Do đó ^AGB < ^GAB, mà ^AGB = ^HAC (câu a) nên ^HAC < ^GAB (1).
Tam giác AGH cân tại A, đường trung tuyến AM => ^GAM = ^HAM (2).
Từ (1) và (2) => ^BAM = ^GAM - ^GAB < ^HAM - ^HAC = ^MAC.
c) Từ câu a => tam giác AGH cân tại A, đường trung tuyến AM đồng thời là đường cao nên AM vuông góc GH.
Hai đường cao BE, CF cắt nhau tại O nên O là trực tâm của tam giác ABC. Do đó AO vuông góc BC.
AM cắt BC tại K, ta thấy ^OAM = 90 độ - ^AKB; ^BNG = 90 độ - ^MKN; hai góc AKB và MIN đối đỉnh với nhau nên ^OAM = ^BNG.
Ý sau đợi mình suy nghĩ ^^^