Question

[Công chúa Lọ Lem]

Cho đường thẳng x;y đi qua O .Vẽ tia Oz sao cho \(\widehat{xOz}\)=\(135^o\)trên một nửa mặt phẳng bờ xy không chứa Oz kẻ tia Ot sao cho \(\widehat{yOt}\)=\(^{90^o}\).Gọi Ov là tia phân giác của \(\widehat{xOt}\).

a.Chỉ rõ rằng \(\widehat{vOz}\)là góc bẹt.

b.Các góc xOv và yOz có phải là 2 góc đối đỉnh không?Vì sao

Answer 1

[alibaba nguyễn]

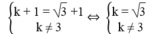
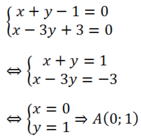
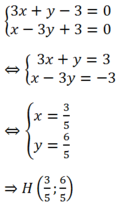
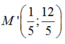
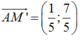
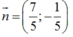
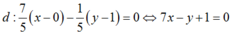
a/ Ta có:

\(\widehat{yOz}=\widehat{xOy}-\widehat{xOz}=180^o-135^o=45^o\)

\(\widehat{xOt}=\widehat{xOy}-\widehat{yOt}=180^o-90^o=90^o\)

\(\Rightarrow\widehat{tOv}=\frac{\widehat{xOt}}{2}=\frac{90^o}{2}=45^o\)

Ta lại có:

\(\widehat{vOz}=\widehat{tOv}+\widehat{yOt}+\widehat{yOz}=45^o+90^o+45^o=180^o\)

\(\Rightarrow\widehat{vOz}\)là góc bẹt.

b/ Vì \(\widehat{vOz}\) là góc bẹt nên Oz và Ov là 2 tia đối nhau

Ta lại có Ox, Oy  là 2 tia đối nhau nên suy ra \(\widehat{xOv},\widehat{yOz}\) là 2 góc đối đỉnh