Tính giá trị biểu thức sau:
A= sin2 20 độ + sin2 30 độ + sin2 40 độ + sin2 70 độ + sin2 60 độ + sin250 độ - tan245 độ
Các bạn giải nhanh giúp mình nhé, mk sẽ hậy tạ sau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
S
8 tháng 8 2021
a) sin230 độ - sin240 độ - sin250 độ + sin2 60 độ
= cos260o - cos250o - sin250o + sin260o
= (cos260o + sin260o) - (cos250o + sin250o)
= 1 - 1 = 0
b) cos225 độ - cos235độ + cos245 độ -cos2 55 độ + cos2 65 độ
= sin265o - sin255o + cos245o - cos255o + cos265o
= (sin265o + cos265o) - (sin255o + cos255o) + cos245o
= 1 - 1 +1/2
= 1/2
2 tháng 5 2016
Bạn biến đổi cuối cùng bằng :A=(sin2\(\alpha\)+\(\cos^2\alpha\))2=12=1
2 tháng 11 2021
\(a,A=\left(\cos^220^0+\cos^270^0\right)+\left(\cos^240^0+\cos^250^0\right)\\ A=\left(\cos^220^0+\sin^220^0\right)+\left(\cos^240^0+\sin^240^0\right)=1+1=2\\ b,B=\left(\cos^2\alpha\right)^3+\left(\sin^2\alpha\right)^3+3\sin^2\alpha\cdot\cos^2\alpha\cdot\left(\sin^2\alpha+\cos^2\alpha\right)\\ B=\left(\sin^2\alpha+\cos^2\alpha\right)^3=1^3=1\)
PT
1
CM
1 tháng 1 2017
Chọn C.
Từ giả thiết ta suy ra:
B = tan2x (sin2x - 1) + sin2 x = -tan2x.cos2x + sin2x
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 2 2021
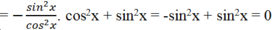
\(S_{HKE}=S_{ABC}-S_{AKE}-S_{BHE}-S_{CHK}\)
\(\Leftrightarrow\dfrac{S_{HKE}}{S_{ABC}}=1-\dfrac{S_{AKE}}{S_{ABC}}-\dfrac{S_{BHE}}{S_{ABC}}-\dfrac{S_{CHK}}{S_{ABC}}\)
\(\Leftrightarrow\dfrac{1}{4}=1-\dfrac{\dfrac{1}{2}AE.AK.sinA}{\dfrac{1}{2}AB.AC.sinA}-\dfrac{\dfrac{1}{2}BH.BE.sinB}{\dfrac{1}{2}AB.BC.sinB}-\dfrac{\dfrac{1}{2}CH.CK.sinC}{\dfrac{1}{2}AC.BC.sinC}\)
\(\Leftrightarrow\dfrac{AE.AK}{AB.AC}+\dfrac{BH.BE}{AB.BC}+\dfrac{CH.CK}{AC.BC}=\dfrac{3}{4}\)
(Để ý rằng \(\dfrac{AE}{AC}=cosA\) do tam giác ACE vuông tại E và tương tự...)
\(\Leftrightarrow cosA.cosA+cosB.cosB+cosC.cosC=\dfrac{3}{4}\)
\(\Leftrightarrow cos^2A+cos^2B+cos^2C=\dfrac{3}{4}\)
\(\Leftrightarrow1-sin^2A+1-sin^2B+1-sin^2C=\dfrac{3}{4}\)
\(\Leftrightarrow sin^2A+sin^2B+sin^2C=\dfrac{9}{4}\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 5 2021
\(P.sina=\dfrac{sina}{sin2a.sina}+\dfrac{sina}{sin3a.sin2a}+...+\dfrac{sina}{sin\left(n+1\right)a.sinna}\)
\(=\dfrac{sin\left(2a-a\right)}{sin2a.sina}+\dfrac{sin\left(3a-2a\right)}{sin3a.sin2a}+...+\dfrac{sin\left[\left(n+1\right)a-na\right]}{sin\left(n+1\right)a.sinna}\)
\(=\dfrac{sin2a.cosa-cos2a.sina}{sin2a.sina}+\dfrac{sin3a.cos2a-cos3a.sin2a}{sin3a.sin2a}+\dfrac{sin\left(n+1\right)a.cosna-cos\left(n+1\right)a.sinna}{sin\left(n+1\right)a.sinna}\)
\(=cota-cot2a+cot2a-cot3a+...+cot\left(na\right)-cot\left(n+1\right)a\)
\(=cota-cot\left(n+1\right)a\)
\(\Rightarrow P=\dfrac{cota-cot\left(n+1\right)a}{sina}\)
A=(sin220°+sin270°)+(sin230°+sin260°)
+(sin240°+sin250°)-tan245°
=(sin220°+cos220°)+(sin230°+cos230°)+(sin240°+cos240°)-1
=1+1+1-1=2
kết quả là 2