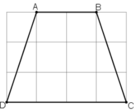
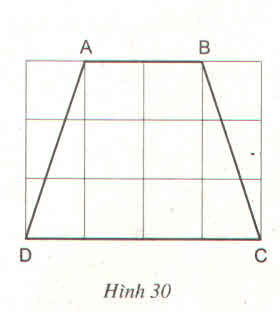
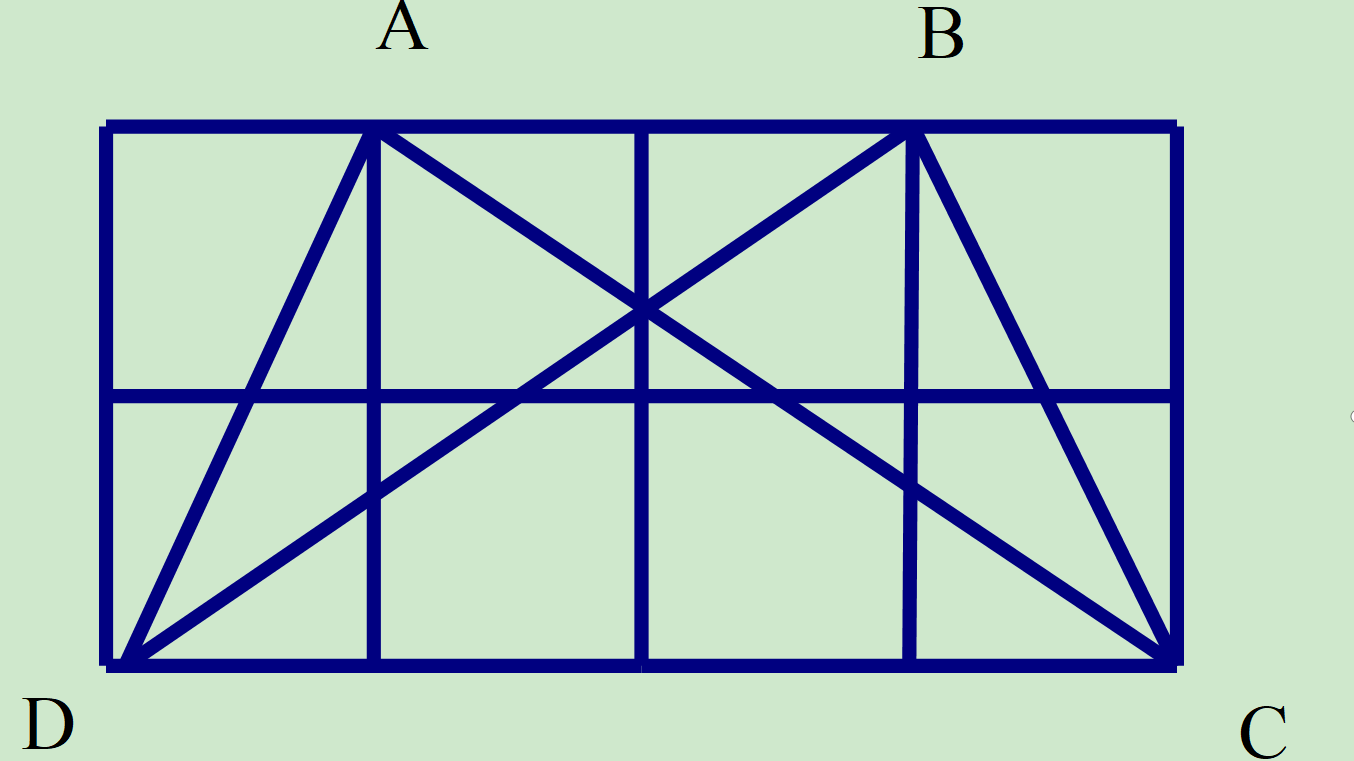
tính độ dài các cạnh của hình thang cân ABCD trên giấy kẻ ô vuông (độ dài của cạnh ô vuông là 1cm)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 8 2019
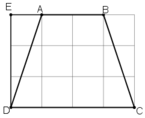
(Mỗi ô vuông là 1cm).
Nhìn vào hình vẽ ta thấy :
+ AB = 2cm
+ CD = 4cm.
+ Tính AD :
Xét tam giác vuông ADE có AE = 1cm, DE = 3cm.
⇒ AD2 = AE2 + DE2 (Định lý Pytago)
= 12 + 32 = 10
⇒ AD = √10 cm
+ Tính BC :
ABCD là hình thang cân nên BC = AD = √10 cm.
Vậy AB = 2cm, CD = 4cm, AD = BC = √10 cm.
21 tháng 4 2017
Bài giải:
Theo hình vẽ, ta có: AB = 2cm, CD = 4cm
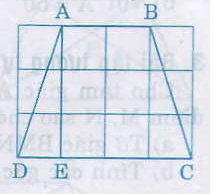
Trong tam giác vuông AED, áp dụng định lý Pitago ta được:
AD2 = AE2 + ED2
= 32 + 12 =10
Suy ra AD = cm
Vậy AB = 2cm, CD = 4cm, AD = BC = cm
26 tháng 10 2017
Áp dụng định lí Pitago :
\(AD^2 = AH^2 + DH^2\)
\(= 3^2 + 1^2\)
\(= 10\)
\(\Rightarrow AD=\sqrt{10}\)
Vậy \(AB = 2cm\);\(CD = 4cm\);\(AD=BC=\sqrt{10}\)
CM
19 tháng 2 2018
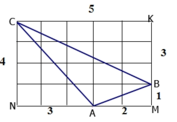
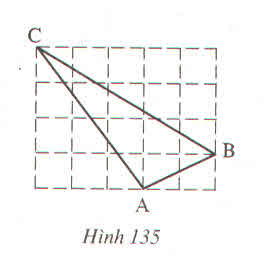
Áp dụng định lí Pi-ta-go trong ΔAMB vuông tại M ta có:
AB2 = AM2 + MB2 = 22 + 12 = 5
⇒ AB = √5
Áp dụng định lí Pi-ta-go trong ΔANC vuông tại N ta có:
AC2 = AN2 + NC2 = 32 + 42 = 25
⇒ AC = 5
Áp dụng định lí Pi-ta-go trong ΔBKC vuông tại K ta có:
BC2 = BK2 + KC2 = 32 + 52 = 34
⇒ BC = √34
23 tháng 1 2021
Gọi mỗi góccòn lại trên giấy ô vuông là K; M; N
Xét Tg AMB vuông tại M ta có:
AB^2 = AM^2 + MB^2 (định lí Pi-ta-go)
Thay số: AB^2 = 22 + 12 = 5
=> AB = căn 5
Xét Tg ANC vuông tại N ta có:
AC^2 = AN^2 + NC^2 (định lí Pi-ta-go )
AC^2= 32 + 42 = 25
=> AC = 5
Xét Tg BKC vuông tại K ta có:
BC^2= BK^2+ KC^2(định lí Pi-ta-go )
BC^2 = 32 + 52 = 34
=>BC= căn 34
TT
20 tháng 4 2017
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34
20 tháng 4 2017
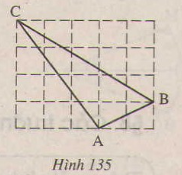
Giải:
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34
Xin lỗi bn mink mới học có lớp 5 thôi à nên MINK ko thể giúp bn, xin lỗi nha
Mk mới học lớp 6 thôi nên mk ko giúp được bạn . Sorry nha !