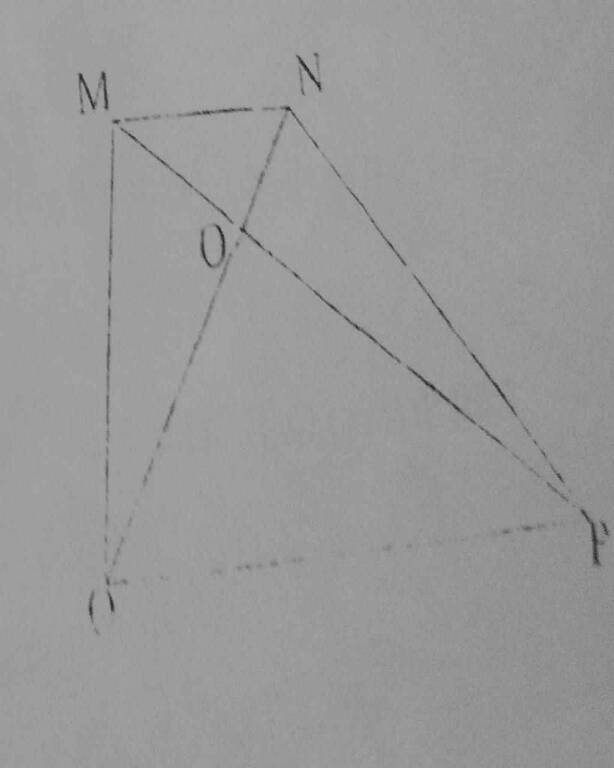
Cho hình thang MNPQ, có đáy bé MN bằng 3/5 đáy lớn PQ. Hai đường chéo MP và NQ cắt nhau tại K. Biết diện tích tam giác NPK là 15cm2. Tính diện tích hình thang MNPQ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

14 tháng 3 2021
Ta có:sADC=sBDC(Vì chung đáy DC và chiều cao đều bằng chiều cao hình hang)
Hai tam giác này lại có chung phần tam giac IDC nên sADI=sBIC=12 cm2
sBIC/sIDC=12/15=4/5
Hai tam giác này có chung chiều cao hạ từ C xuống BD nên BI/ID=sBIC/sDIC=4/5
Hai tam giac AIB và ADI có chung chiều cao hạ từ A xuống DB nên sAIB/sADI=BI/ID=4/5
Suy ra sAIB=4/5x sADI=4/5x12=9,6(cm2)
Vaạy diện tích hình thang là:
12x2+15+9,6=48,6(cm2)
Đáp só:48,6 cm2
k mình nhé
Lời giải:
$S_{MNQ}=S_{MNP}$ (do chiều cao bằng nhau và chung đáy)
$\Rightarrow S_{MQK}=S_{NKP}=15$ (cm2)
Kẻ đường cao $NH$ xuống $MP$, đường cao $QT$ xuông $MH$
\(\frac{S_{MNP}}{S_{MQP}}=\frac{MN}{PQ}=\frac{3}{5}\)
\(\frac{S_{MNP}}{S_{MQP}}=\frac{NH}{QT}\)
\(1=\frac{S_{NPK}}{S_{MQK}}=\frac{NH\times PK}{QT\times MK}\Rightarrow \frac{NH}{QT}=\frac{MK}{PK}\)
Từ 3 điều trên suy ra $\frac{MK}{PK}=\frac{3}{5}$
$\frac{S_{MNK}}{S_{NPK}}=\frac{MK}{PK}=\frac{3}{5}$
$S_{MNK}=\frac{3}{5}\times S_{NPK}=\frac{3}{5}\times 15=9$ (cm2)
$\frac{S_{MQK}}{S_{PQK}}=\frac{MK}{PK}=\frac{3}{5}$
$\Rightarrow S_{PQK}=\frac{5}{3}\times S_{MQK}=\frac{5}{3}\times 15=25$ (cm2)
Diện tích hình thang:
$15+15+9+25=64$ (cm2)
Hình vẽ: