a) tìm n \(\in\)N để (2n-1)\(⋮\)7
b) chứng minh n6+n4-2n2 \(⋮\)72 \(\forall\)n\(\in\)Z
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 12 2021
a, Với n = 1 ta có 3 ⋮ 3.
Giả sử n = k ≥ 1 , ta có : k3 + 2k ⋮ 3 ( GT qui nạp).
Ta đi chứng minh : n = k + 1 cũng đúng:
(k+1)^3 + 2(k+1) = k^3 + 3k^2 + 3k + 1 + 2k + 2
= (k^3+2k) + 3(k^2+k+1)
Ta có : + (k^3+2k) ⋮ 3 ( theo gt trên)
+ 3(k^2+k+1) hiển nhiên chia hết cho 3
Vậy mệnh đề luôn chia hết cho 3.
b, Với n = 1 ta có 12 ⋮ 6.
Giả sử n = k ≥ 1 , ta có: 13k -1 ⋮ 6
Ta đi chứng minh : n = k+1 cũng đúng:
=> 13k.13 - 1 = 13(13k - 1) + 12.
Có: - 13(13k - 1) ⋮ 6 ( theo gt)
- 12⋮6 ( hiển nhiên)
> Vậy mệnh đề luôn đúng.
3 tháng 7 2023
1:
2n^2+5n-1 chia hết cho 2n-1
=>2n^2-n+6n-3+2 chia hết cho 2n-1
=>2n-1 thuộc {1;-1;2;-2}
mà n nguyên
nên n=1 hoặc n=0
2:
a: A=n(n+1)(n+2)
Vì n;n+1;n+2 là 3 số liên tiếp
nên A=n(n+1)(n+2) chia hết cho 3!=6
b: B=(2n-1)[(2n-1)^2-1]
=(2n-1)(2n-2)*2n
=4n(n-1)(2n-1)
Vì n;n-1 là hai số nguyên liên tiếp
nên n(n-1) chia hết cho 2
=>B chia hết cho 8
c: C=n^2+14n+49-n^2+10n-25=24n+24=24(n+1) chia hết cho 24
CY
1
AH
Akai Haruma
Giáo viên
18 tháng 12 2021
Lời giải:
$7.2^{2n-2}\equiv 2.2^{2n-2}\equiv 2^{2n-1}\pmod 5$
$\Rightarrow 7.2^{2n-2}+3^{2n-1}\equiv 2^{2n-1}+3^{2n-1}\pmod 5$
Mà $2^{2n-1}+3^{3n-1}\vdots (2+3=5)$ (do $2n-1$ lẻ)
$\Rightarrow 7.2^{2n-2}+3^{2n-1}\vdots 5$ (đpcm)
CM
9 tháng 5 2017
Cách 1: Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
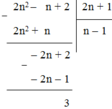
2n2 – n + 2 chia hết cho 2n + 1
⇔ 3 ⋮ (2n + 1) hay (2n + 1) ∈ Ư(3)
⇔ 2n + 1 ∈ {±1; ±3}
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Cách 2:
Ta có:
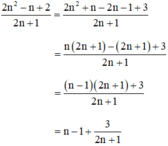
2n2 – n + 2 chia hết cho 2n + 1
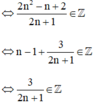
⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.
Để (2^n-1);7 thì nó phải thuộc U(7) =1:-1;7;-7
Vậy n=3 thì (2^n-1);7