6. Biết rằng phương trình x 3 −3x 2 +3 = 0 có ba nghiệm phân biệt. Chứng minh rằng trong ba nghiệm này có hai nghiệm a,b thoả mãn ab+3 = a+2b.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

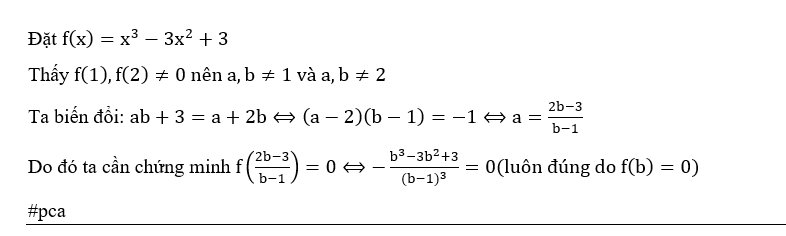

* Giả sử cả 3 pt đều có nghiệm kép hoặc vô nghiệm ta có :
pt \(x^2-2ax+b=0\) (1) có \(\Delta_1'=\left(-a\right)^2-b=a^2-b\le0\)
pt \(x^2-2bx+c=0\) (2) có \(\Delta_2'=\left(-b\right)^2-c=b^2-c\le0\)
pt \(x^2-2cx+a=0\) (3) có \(\Delta_3'=\left(-c\right)^2-a=c^2-a\le0\)
\(\Rightarrow\)\(\Delta_1'+\Delta_2'+\Delta_3'=\left(a^2+b^2+c^2\right)-\left(a+b+c\right)\le0\) (*)
Lại có : \(0< a,b,c< 3\)\(\Rightarrow\)\(\hept{\begin{cases}a\left(3-a\right)>0\\b\left(3-b\right)>0\\c\left(3-c\right)>0\end{cases}\Leftrightarrow\hept{\begin{cases}3a>a^2\\3b>b^2\\3c>c^2\end{cases}}}\)
\(\Rightarrow\)\(\left(a^2+b^2+c^2\right)-\left(a+b+c\right)< 3\left(a+b+c\right)-\left(a+b+c\right)=2\left(a+b+c\right)=6>0\)
trái với (*)
Vậy có ít nhất một phương trình có hai nghiệm phân biệt
cái kia chưa bt làm -_-

a) \(\Delta=\left[-\left(m+3\right)\right]^2-4.1.m\\ =m^2+6m+9-4m\\ =m^2+2m+9\\ =\left(m+1\right)^2+8>0\forall m\)
Vậy phương trình luôn có 2 nghiệm phân biệt với mọi m.
b) Áp dụng hệ thức Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1x_2=m\end{matrix}\right.\)
Mà \(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\\ \Leftrightarrow\left(m+3\right)^2-2m=6\\ \Leftrightarrow m^2+6m+9-2m=6\\ \Leftrightarrow m^2+4m+3=0\\ \Leftrightarrow\left(m+1\right)\left(m+3\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)
Vậy \(m\in\left\{-1;-3\right\}\) là các giá trị cần tìm.
a, Ta có: \(\Delta=\left[-\left(m+3\right)\right]^2-4.1.m\)
\(=m^2+6m+9-4m\)
\(=m^2+2m+9\)
\(=m^2+2m+1+8\)
\(=\left(m+1\right)^2+8\)
Lại có: \(\left(m+1\right)^2\ge0\forall m\Rightarrow\left(m+1\right)^2+8\ge8\forall m\)
Vậy phương trình luôn có 2 nghiêm phân biệt
b, Theo hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=m+3\\x_1+x_2=m\end{matrix}\right.\)
Theo bài ra:
\(x_1^2+x_2^2=6\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=6\)
\(\Leftrightarrow\left(m+3\right)^2-2m=6\)
\(\Leftrightarrow m^2+6m+9-2m=6\)
\(\Leftrightarrow m^2+6m+9-2m-6=0\)
\(\Leftrightarrow m^2+4m+3=0\)
\(\Leftrightarrow m^2+m+3m+3=0\)
\(\Leftrightarrow\left(m^2+m\right)+\left(3m+3\right)=0\)
\(\Leftrightarrow m\left(m+1\right)+3\left(m+1\right)=0\)
\(\Leftrightarrow\left(m+1\right)\left(m+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m+1=0\\m+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=-3\end{matrix}\right.\)
Vậy với m=-1 hoặc m=-3 thì phương trinh trên thỏa mãn hệ thức

- Dễ dàng nhận thấy \(x=-1\) không phải là 1 nghiệm của đa thức P(x).
- Gọi b là 1 nghiệm của đa thức \(P\left(x\right)=x^3+3x^2-1\)
Do đó: \(b^3+3b^2-1=0\)
\(\Rightarrow\left(b^3+3b^2+3b+1\right)-3\left(b+1\right)+1=0\)
\(\Rightarrow\left(b+1\right)^3-3\left(b+1\right)+1=0\)
\(\Rightarrow\dfrac{\left(b+1\right)^3-3\left(b+1\right)+1}{\left(b+1\right)^3}=0\)
\(\Rightarrow\left(\dfrac{1}{b+1}\right)^3-3.\left(\dfrac{1}{b+1}\right)^2+1=0\)
\(\Rightarrow\left(-\dfrac{1}{b+1}\right)^3+3.\left(-\dfrac{1}{b+1}\right)^2-1=0\)
Thay \(x=-\dfrac{1}{b+1}\) vào \(P\left(x\right)=x^3+3x^2-1\) ta được:
\(P\left(-\dfrac{1}{b+1}\right)=\left(-\dfrac{1}{b+1}\right)^3+3.\left(-\dfrac{1}{b+1}\right)^2-1=0\)
\(\Rightarrow-\dfrac{1}{b+1}\) là một nghiệm của đa thức P(x).
Đặt \(a=-\dfrac{1}{b+1}\Rightarrow ab+a+1=0\) \(\Rightarrowđpcm\)

bài này dễ mà
a 0 thay m vào tìm đk x
b, xét 2th
+) vs m=-2 thay vào giải tìm ra x
+) vs m khác -2 tính đen -ta cm cho nó lớn hơn hoặc bằng 0
c. áp dụng vi-ét , tính \(3x_1=2x_2\)
