A - ( 2xy + 4y2) = 3x2 - 6xy +...
Đọc tiếp
A - ( 2xy + 4y2) = 3x2 - 6xy + 5y2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 7 2020
Đề nhìn như này khó hiểu lắm. Bạn có thể viết lại đề không
Chúc bạn học tốt
27 tháng 9 2021
a: Ta có: \(A=x^2-2xy+5y^2+4y+51\)
\(=x^2-2xy+y^2+4y^2+4y+1+50\)
\(=\left(x-y\right)^2+\left(2y+1\right)^2+50\ge50\forall x,y\)
Dấu '=' xảy ra khi \(x=y=-\dfrac{1}{2}\)
27 tháng 9 2021
a) \(A=x^2-2xy+5y^2+4y+51=\left(x^2-2xy+y^2\right)+\left(4y^2+4y+1\right)+50=\left(x-y\right)^2+\left(2y+1\right)^2+50\ge50\)
\(minA=50\Leftrightarrow x=y=-\dfrac{1}{2}\)
c) \(C=\dfrac{9}{-2x^2+4x-7}=\dfrac{9}{-2\left(x^2-2x+1\right)-5}=\dfrac{9}{-2\left(x-1\right)^2-5}\ge\dfrac{9}{-5}=-\dfrac{9}{5}\)
\(minC=-\dfrac{9}{5}\Leftrightarrow x=1\)
d) \(10x^2+4y^2-4xy+8x-4y+20=\left[4y^2-4y\left(x+1\right)+\left(x+1\right)^2\right]+\left(9x^2+6x+1\right)+18=\left(2y-x-1\right)^2+\left(3x+1\right)^2+18\ge18\)
\(minD=18\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-\dfrac{1}{3}\\y=\dfrac{1}{3}\end{matrix}\right.\)
e) \(E=9x^2+2y^2+6xy-6x-8y+10=\left[9x^2+6x\left(y-1\right)+\left(y-1\right)^2\right]+\left(y^2-6x+9\right)=\left(3x+y-1\right)^2+\left(y-3\right)^2\ge0\)
\(minE=0\Leftrightarrow\) \(\left\{{}\begin{matrix}x=-\dfrac{2}{3}\\y=3\end{matrix}\right.\)
5 tháng 9 2021
\(a,9x^2+y^2+2z^2-18x+4z-6y+20=0\\ \Leftrightarrow9\left(x-1\right)^2+\left(y-3\right)^2+2\left(z+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\\z=-1\end{matrix}\right.\)
\(b,5x^2+5y^2+8xy+2y-2x+2=0\\ \Leftrightarrow4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=-y\\x=1\\y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(c,5x^2+2y^2+4xy-2x+4y+5=0\\ \Leftrightarrow\left(2x+y\right)^2+\left(x-1\right)^2+\left(y+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}2x=-y\\x=1\\y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(d,x^2+4y^2+z^2=2x+12y-4z-14\\ \Leftrightarrow\left(x-1\right)^2+\left(2y-3\right)^2+\left(z+2\right)^2=0\\ \Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\dfrac{3}{2}\\z=-2\end{matrix}\right.\)
\(e,x^2+y^2-6x+4y+2=0\\ \Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
Pt vô nghiệm do ko có 2 bình phương số nguyên có tổng là 11
5 tháng 9 2021
e: Ta có: \(x^2-6x+y^2+4y+2=0\)
\(\Leftrightarrow x^2-6x+9+y^2+4y+4-11=0\)
\(\Leftrightarrow\left(x-3\right)^2+\left(y+2\right)^2=11\)
Dấu '=' xảy ra khi x=3 và y=-2
AH
Akai Haruma
Giáo viên
24 tháng 11 2021
a.
$12x^3y-24x^2y^2+12xy^3=12xy(x^2-2xy+y^2)=12xy(x-y)^2$
b.
$x^2-6x+xy-6y=(x^2+xy)-(6x+6y)=x(x+y)-6(x+y)=(x-6)(x+y)$
c.
$2x^2+2xy-x-y=2x(x+y)-(x+y)=(x+y)(2x-1)$
d.
$x^3-3x^2+3x-1=(x-1)^3$
e.
$3x^2-3y^2-12x-12y=(3x^2-3y^2)-(12x+12y)$
$=3(x-y)(x+y)-12(x+y)=(x+y)[3(x-y)-12]=3(x-y)(x-y-4)$
f.
$x^2-2xy-x^2+4y^2=4y^2-2xy=2y(2y-x)$
C
1
28 tháng 4 2021
a) M - \(^{\left(x^2y-1\right)}\)= -2\(x^3\)+\(x^2y\)+1
=> M= (-2\(x^3\)+\(x^2y\)+1) + \(^{\left(x^2y-1\right)}\)
=> M= -2\(x^3\)+\(x^2y\)+1+ \(^{x^2y-1}\)
=> M= -2\(x^3\)+(\(x^2y+x^2y\))+1-1
=> M= -2\(x^3\)+\(2x^2y\)
b) \(3x^2+3xy-3x^3-M=3x^2+2xy-4y^2\)
=> \(M=\left(3x^2+3xy-3x^3\right)-\left(3x^2+2xy-4y^2\right)\)
\(=>M=3x^2+3xy-3x^3-3x^2-2xy+4y^2\)
\(=>M=\left(3x^2-3x^2\right)+\left(3xy-2xy\right)-3x^3+4y^2\)
\(=>M=xy-3x^3+4y^2\)
Hơi muộn nhưng mong bạn tick cho mình 
1 tháng 10 2021
a) \(4x^3y^2-8x^2y+12xy^2=4xy\left(x^2y-2x+3y\right)\)
b) \(3x^2-6xy-5x+10y=3x\left(x-2y\right)-5\left(x-2y\right)=\left(x-2y\right)\left(3x-5\right)\)
c) \(x^2-49+4y^2-4xy=\left(x-2y\right)^2-49=\left(x-2y-7\right)\left(x-2y+7\right)\)
d) \(x^2-6x-16=\left(x^2-6x+9\right)-25=\left(x-3\right)^2-25=\left(x-3-5\right)\left(x-3+5\right)=\left(x-8\right)\left(x+2\right)\)
Q
1 tháng 10 2021
a) 4x3y2−8x2y+12xy2=4xy(x2y−2x+3y)4x3y2−8x2y+12xy2=4xy(x2y−2x+3y)
b) 3x2−6xy−5x+10y=3x(x−2y)−5(x−2y)=(x−2y)(3x−5)3x2−6xy−5x+10y=3x(x−2y)−5(x−2y)=(x−2y)(3x−5)
c) x2−49+4y2−4xy=(x−2y)2−49=(x−2y−7)(x−2y+7)x2−49+4y2−4xy=(x−2y)2−49=(x−2y−7)(x−2y+7)
d) x2−6x−16=(x2−6x+9)−25=(x−3)2−25=(x−3−5)(x−3+5)=(x−8)(x+2)
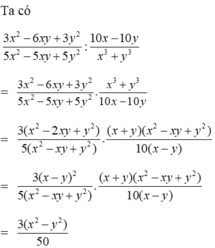
\(A-\left(2xy+4y^2\right)=3x^2-6xy+5y^2\\ \Leftrightarrow A=3x^2-6xy+5y^2+2xy+4y^2=3x^2-4xy+9y^2\)