Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Tam giác `ABC` có \(\widehat{A}=64^0\)
Mà `AD` là tia phân giác của \(\widehat{BAC}\)
`->`\(\widehat{BAD}=\widehat{CAD}=\)`64/2=32^0`
Xét Tam giác `BAD:`
\(\widehat{BAD}+\widehat{ADB}+\widehat{ABD}=180^0 (\text {Định lý tổng 3 góc trong 1 tam giác})\)
\(32^0+\widehat{ADB}+80^0=180^0\)
`->`\(\widehat{ADB}=180^0-80^0-32^0=68^0\)
Xét các đáp án trên `->` \(\text{D. (t/m)}\)
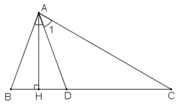
Trong ΔABC có:
∠(BAC) + ∠B + ∠C = 180o (tổng ba góc trong tam giác)
Mà ∠(BAC) + 70o + 30o = 180
Vậy ∠(BAC) = 180o-70o - 30o = 80o
Ta có AD là tia phân giác của ∠(BAC) nên ∠(BAD) = 32o
Trong tam giác ABD có ∠(ADB) = 180o - 32o - 80o = 68o. Chọn C
* Ghi đề thiếu kìa :(
\(\text{Xét}\)\(\Delta ABC\)\(\text{ta có:}\)
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\rightarrow\widehat{C}=180^o-64^o-80^o\)
\(\rightarrow\widehat{C}=36^o\)
\(\text{Mà tia}\)\(AD\)\(\text{là tia phân giác của}\)\(\widehat{A}\)
\(\rightarrow\widehat{DAB}=64^o:2\)
\(\rightarrow\widehat{DAB}=32^o\)
\(\text{Xét}\)\(\Delta ADB\)\(\text{ta có:}\)
\(\rightarrow\widehat{DAB}+\widehat{B}+\widehat{ADB}=180^o\)
\(\rightarrow\widehat{ADB}=180^o-80^o-32^o\)
\(\rightarrow\widehat{ADB}=68^o\)
Số đo góc nào bạn?